题目内容
8.已知双曲线:x2-$\frac{{y}^{2}}{4}$=1上一点P到它的一个焦点的距离为2,则它到另一个焦点的距离为( )| A. | 3 | B. | 4 | C. | 6 | D. | 2+2$\sqrt{5}$ |
分析 先根据条件求出a=1;再根据双曲线定义得到关于所求距离d的等式即可得到结论.
解答 解:设所求距离为d,由题得:a=1.
根据双曲线的定义得:2a=d-2⇒d=2a+2=4.
故选:B.
点评 本题主要考查双曲线的定义.在解决涉及到圆锥曲线上的点与焦点之间的关系的问题中,圆锥曲线的定义往往是解题的突破口.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线与直线x=$\frac{{a}^{2}}{c}$交于点M,设其右焦点为F,且点F到渐近线的距离为d,则( )
| A. | |MF|>d | B. | |MF|<d | C. | |MF|=d | D. | 与a,b的值有关 |
20.对于满足|f(n+1)-f(n)|≤($\frac{1}{10}$)n(n∈N)的所有f(n),若f(0)=1,则f(10)的值所在的区间一定是( )
| A. | (-1,1) | B. | (0,2) | C. | (-$\frac{1}{9}$,$\frac{19}{9}$) | D. | (-$\frac{1}{5}$,$\frac{9}{5}$) |
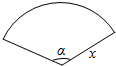 如图,用一根长为10m绳索围成了一个圆心角小于x且半径不超过3m的扇形场地,设扇形的半径为xm,面积为Scm2.
如图,用一根长为10m绳索围成了一个圆心角小于x且半径不超过3m的扇形场地,设扇形的半径为xm,面积为Scm2.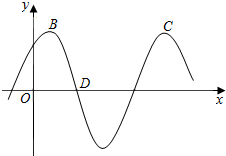 如图所示,B,C两点是函数f(x)=Asin(2x+$\frac{π}{3}$)(A>0)图象上相邻的两个最高点,D点为函数f(x)图象与x轴的一个交点.
如图所示,B,C两点是函数f(x)=Asin(2x+$\frac{π}{3}$)(A>0)图象上相邻的两个最高点,D点为函数f(x)图象与x轴的一个交点.