题目内容
13.已知$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(-3,2),当实数k为何值时,(Ⅰ)k$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$-3$\overrightarrow{b}$垂直?
(Ⅱ)k$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$-3$\overrightarrow{b}$平行?平行时它们是同向还是反向?
分析 (1)利用向量垂直与数量积的关系即可得出;
(2)利用向量共线定理即可得出.
解答 解:$k\overrightarrow a+\vec b=k(1,2)+(-3,2)=(k-3,2k+2)$$\overrightarrow a-3\vec b=(1,2)-3(-3,2)=(10,-4)$,
(1)∵$(k\overrightarrow a+\vec b)⊥$$(\overrightarrow a-3\vec b)$,
得$(k\overrightarrow a+\vec b)•$$(\overrightarrow a-3\vec b)=10(k-3)-4(2k+2)=2k-38=0,k=19$.
(2)∵$(k\overrightarrow a+\vec b)∥$$(\overrightarrow a-3\vec b)$,得$-4(k-3)=10(2k+2),k=-\frac{1}{3}$,
此时$k\overrightarrow a+\vec b=(-\frac{10}{3},\frac{4}{3})=-\frac{1}{3}(10,-4)$,所以方向相反.
点评 本题考查了向量垂直与数量积的关系、向量共线定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
8.已知点A(2,4),向量$\overrightarrow{a}$=(3,4),且$\overrightarrow{AB}$=2$\overrightarrow{a}$,则点B的坐标为(8,12).
2.已知直线l1:x-2y-1=0,直线l2:ax-by+1=0,a,b∈{1,2,3,4},则直线l1与直线l2没有公共点的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{8}$ | D. | $\frac{3}{16}$ |
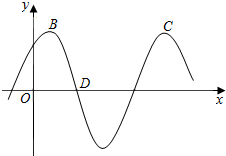 如图所示,B,C两点是函数f(x)=Asin(2x+$\frac{π}{3}$)(A>0)图象上相邻的两个最高点,D点为函数f(x)图象与x轴的一个交点.
如图所示,B,C两点是函数f(x)=Asin(2x+$\frac{π}{3}$)(A>0)图象上相邻的两个最高点,D点为函数f(x)图象与x轴的一个交点.