题目内容
10.数列{an}的前n项和记为Sn,已知2Sn=3an-2,求an.分析 由已知数列递推式求出首项,并得到当n≥2时的递推式,和原递推式作差后,可得数列{an}是以2为首项,以3为公比的等比数列,再由等比数列的通项公式得答案.
解答 解:由2Sn=3an-2,得2a1=3a1-2,即a1=2.
当n≥2时,2Sn-1=3an-1-2,
两式作差得:2an=3an-3an-1,即an=3an-1(n≥2).
∴数列{an}是以2为首项,以3为公比的等比数列.
则${a}_{n}=2•{3}^{n-1}$.
点评 本题考查数列递推式,考查了等比关系的确定,考查等比数列的通项公式,是中档题.

练习册系列答案
相关题目
20.A、B、C、D四人站成一排照相,A和B必须站在一起的站法有( )种.
| A. | 6 | B. | 12 | C. | 24 | D. | 8 |
18.若函数f(x)=$\left\{\begin{array}{l}{2,x<0}\\{{x}^{2}-2ax+a,x≥0}\end{array}\right.$ 的图象上恰好有两对关于原点对称的点,则实数a的取值范围是( )
| A. | (1,2) | B. | (2,+∞) | C. | (-2,1) | D. | (-2,+∞) |
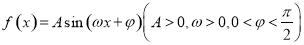 的图象经过三点
的图象经过三点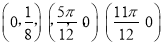 ,且在区间
,且在区间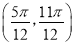 内有唯一的最值,且为最小值.
内有唯一的最值,且为最小值.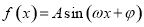 的解析式;
的解析式;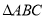 中,
中,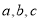 分别是角
分别是角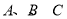 的对边,若
的对边,若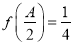 且
且 ,求
,求 的值.
的值.