题目内容
5.已知|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=2,且|$\overrightarrow{a}$+$\overrightarrow{b}$|≤x2-2x恒成立,求x的取值范围.分析 设$\overrightarrow{a},\overrightarrow{b}$夹角为θ,用θ表示出|$\overrightarrow{a}+\overrightarrow{b}$|,令|$\overrightarrow{a}+\overrightarrow{b}$|的最大值小于或等于x2-2x的最小值即可.
解答 解:∵|$\overrightarrow{a}$+$\overrightarrow{b}$|≤|$\overrightarrow{a}$|+|$\overrightarrow{b}$|=3,
∴3|≤x2-2x,即x2-2x-3≥0,解得x≤-1,或x≥3.
∴x的取值范围是(-∞,-1]∪[3,+∞).
点评 本题考查了平面向量的数量积运算及向量模运算,是基础题.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
16.某几何体的三视图如图所示,则该几何体的体积为( )
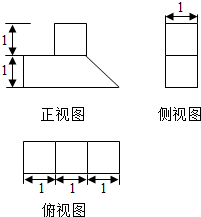

| A. | 2 | B. | $\frac{5}{2}$ | C. | 3 | D. | $\frac{7}{2}$ |
14.设抛物线y2=16x的焦点为F,点P在此抛物线上,且横坐标为5,则|PF|等于( )
| A. | 13 | B. | 8 | C. | 9 | D. | 10 |
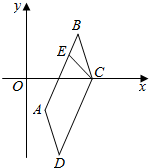 如图,在平行四边形ABCD中,边AB所在的直线方程为2x-y-2=0,点C(2,0),D(1,t),t∈R.
如图,在平行四边形ABCD中,边AB所在的直线方程为2x-y-2=0,点C(2,0),D(1,t),t∈R.