Question

18．已知函数f（x）=$\sqrt{2}$sin（2x+$\frac{π}{4}$）．
（1）求f（x）的单调递增区间；
（2）若函数g（x）=f（x）-k在[0，$\frac{π}{2}$]上有两个不同的零点，求实数k的取值范围．

Answer 1

分析 （1）由条件利用正弦函数的单调性求得f（x）的单调递增区间．
（2）由题意可得即 f（x）的图象和直线y=k在[0，$\frac{π}{2}$]上有两个不同的交点，数形结合可得k的范围．

解答 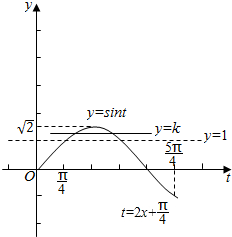解：（1）对于函数f（x）=$\sqrt{2}$sin（2x+$\frac{π}{4}$），
令2kπ-$\frac{π}{2}$≤2x+$\frac{π}{4}$≤2kπ+$\frac{π}{2}$，
求得kπ-$\frac{3π}{8}$≤x≤kπ+$\frac{π}{8}$，可得函数的增区间为[kπ-$\frac{3π}{8}$，kπ+$\frac{π}{8}$]，
k∈Z．
（2）函数g（x）=f（x）-k在[0，$\frac{π}{2}$]上有两个不同的零点，
即 f（x）的图象和直线y=k在[0，$\frac{π}{2}$]上有两个不同的交点．
由x∈[0，$\frac{π}{2}$]，可得 2x+$\frac{π}{4}$∈[$\frac{π}{4}$，$\frac{5π}{4}$]，
结合图象可得1≤k＜$\sqrt{2}$．

点评 本题主要考查正弦函数的单调性，正弦函数的图象特征，方程根的存在性以及个数判断，体现了数形结合的数学思想，属于中档题．