题目内容
已知集合A={x|x=sin
，k∈Z}，B={x||x-1|≤1}，则A∩B=（ ）
| kπ |
| 2 |
| A、{-1，0} | B、{1，0} |
| C、{0} | D、{1} |
考点：交集及其运算
专题：集合
分析：求出集合A，B，根据集合的基本运算即可．
解答：
解：A={x|x=sin
，k∈Z}={0，-1，1}，B={x||x-1|≤1}={x|0≤x≤2}，
则A∩B={0，1}，
故选：B
| kπ |
| 2 |
则A∩B={0，1}，
故选：B
点评：本题主要考查集合的基本运算，根据不等式的解法求出集合A，B是解决本题的关键．
练习册系列答案
相关题目
数列{an}为等差数列，若a2+a8=
π，则tan（a3+a7）的值为（ ）
| 2 |
| 3 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
函数f（x）=lg（1-x）的定义域为（ ）
| A、[0，1] |
| B、（-1，+∞） |
| C、[-1，1] |
| D、（-∞，1） |
设集合A={x|y=
}，B={y|y=2x，x＞1}，则A∩B为（ ）
| 3x-x2 |
| A、[0，3] |
| B、（2，3] |
| C、[3，+∞） |
| D、[1，3] |
直线kx-y+3k-2=0恒过一定点，则该定点的坐标（ ）
| A、（3，2） |
| B、（-3，-2） |
| C、（2，3） |
| D、（-2，-3） |
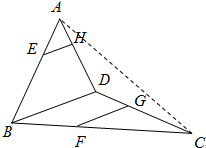如图，空间四边形ABCD中，E、H为AB、AD的中点，G、F为BC、CD上的点，且