题目内容
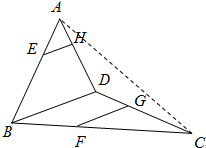 如图,空间四边形ABCD中,E、H为AB、AD的中点,G、F为BC、CD上的点,且
如图,空间四边形ABCD中,E、H为AB、AD的中点,G、F为BC、CD上的点,且| CF |
| CB |
| CG |
| CD |
(Ⅰ)证明:EH∥BD;
(Ⅱ)若FE∩GH=M,判断点M是否在直线AC上,并证明你的结论.
考点:平面的基本性质及推论
专题:空间位置关系与距离
分析:(Ⅰ)由三角形的中位线即可证明结论成立;
(Ⅱ)先证明点M在直线AC上,即M在平面ABC内,也在平面ADC内,即证在两平面的交线上.
(Ⅱ)先证明点M在直线AC上,即M在平面ABC内,也在平面ADC内,即证在两平面的交线上.
解答:
(Ⅰ)证明:∵E、H为AB、AD的中点,
∴EH∥BD;
(Ⅱ)当FE∩GH=M时,点M在直线AC上,
证明如下:∵FE∩GH=M,
∴M∈FE,M∈GH;
又∵F∈BC,E∈AB,∴EF?平面ABC;
∴M∈平面ABC;
同理,M∈平面ADC;
又∵平面ABC∩平面ADC=AC,
∴M∈AC;
即点M在直线AC上.
点M在直线AC上.
∴EH∥BD;
(Ⅱ)当FE∩GH=M时,点M在直线AC上,
证明如下:∵FE∩GH=M,
∴M∈FE,M∈GH;
又∵F∈BC,E∈AB,∴EF?平面ABC;
∴M∈平面ABC;
同理,M∈平面ADC;
又∵平面ABC∩平面ADC=AC,
∴M∈AC;
即点M在直线AC上.
点M在直线AC上.
点评:本题考查了平面的基本公理与推理的应用问题,解题时应结合图形进行解答,是基础题目.

练习册系列答案
相关题目
已知函数f(x)=
,若f(x)=
,则x的值为( )
|
| 1 |
| 3 |
A、
| |||
B、
| |||
C、
| |||
| D、-1 |
已知集合A={x|x=sin
,k∈Z},B={x||x-1|≤1},则A∩B=( )
| kπ |
| 2 |
| A、{-1,0} | B、{1,0} |
| C、{0} | D、{1} |
已知复数z=
,则( )
| 2 |
| -1+i |
| A、z的实部为1 |
| B、z的虚部为-i |
| C、z的虚部为-1 |
| D、z的共轭复数为1+i |
复数
等于( )
| 2+i |
| i |
| A、1+2i | B、1-2i |
| C、-1+2i | D、-1-2i |
在△ABC中,|
|=2,|
|=1,已知D是BC边上一点,AD平分∠BAC,
=λ
+μ
则( )
| AB |
| AC |
| AD |
| AB |
| AC |
A、λ=
| ||||
B、λ=
| ||||
C、λ=
| ||||
D、λ=
|
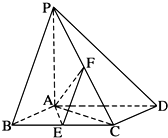 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.