题目内容
若a=sin46°，b=cos46°，c=cos36°，则a、b、c由小到大的顺序为 ．
考点：余弦函数的图象,正弦函数的图象
专题：三角函数的图像与性质
分析：根诱导公式结合余弦函数的单调性即可得到结论．
解答：
解：sin46°=cos44°，
∵y=cosx在0°＜x＜90°上是减函数，
∴cos46°＜cos44°＜cos36°，
故b＜a＜c，
故答案为：b＜a＜c
∵y=cosx在0°＜x＜90°上是减函数，
∴cos46°＜cos44°＜cos36°，
故b＜a＜c，
故答案为：b＜a＜c
点评：本题主要考查函数值的大小比较，利用诱导公式以及三角函数的单调性是解决本题的关键．
练习册系列答案
相关题目
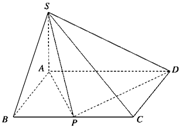如图，四棱锥S-ABCD的底面是矩形，SA⊥底面ABCD，P为BC边的中点，AD=2，SA=AB=1．则PD与平面SAP所成的角的大小为已知集合A={a，b}，B={-5，0，5}，对应关系f是从集合A到集合B的一个映射，则满足条件f（a）+f（b）=0的映射有（ ）
| A、3个 | B、4个 | C、5个 | D、6个 |