题目内容
定义:区间[a,b](a<b)的长度为b-a,已知函数f(x)=|(x+1) -
-1|的定义域为[a,b],值域为[0,
],则区间[a,b]长度的最大值为 .
| 1 |
| 2 |
| 1 |
| 2 |
考点:函数的最值及其几何意义
专题:函数的性质及应用
分析:可以先做出函数f(x)=|(x+1) -
-1|(x≠-1)的图象,找到其介于直线y=0与直线y=
之间的图象,据图可以求出区间[a,b]长度的最大值.
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:做出函数f(x)=|(x+1) -
-1|的图象如下:(可由函数y=x -
的图象先向左平移一个单位,再沿x轴向下平移一个单位,x轴上方图象不变,将x轴以下的部分对称到x轴上方来,即可得到所求函数图象.
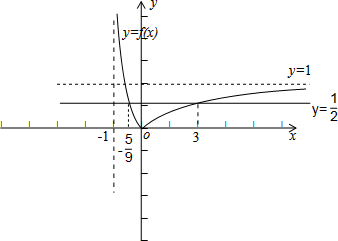
因为值域为[0,
],且f(0)=0,所以0∈[a,b],又因为f(3)=f(-
)=
,
所以b-a的最大值为3-(-
)=
.
故答案为:
.
| 1 |
| 2 |
| 1 |
| 2 |
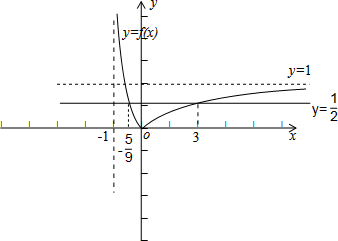
因为值域为[0,
| 1 |
| 2 |
| 5 |
| 9 |
| 1 |
| 2 |
所以b-a的最大值为3-(-
| 5 |
| 9 |
| 32 |
| 9 |
故答案为:
| 32 |
| 9 |
点评:本题主要是考查利用函数图象解决有关函数性质的问题,体现了数形结合的思想;注意图象的画法,如渐近线等,画图要准确.

练习册系列答案
相关题目
已知集合A={a,b},B={-5,0,5},对应关系f是从集合A到集合B的一个映射,则满足条件f(a)+f(b)=0的映射有( )
| A、3个 | B、4个 | C、5个 | D、6个 |
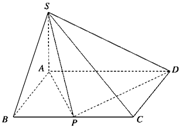 如图,四棱锥S-ABCD的底面是矩形,SA⊥底面ABCD,P为BC边的中点,AD=2,SA=AB=1.则PD与平面SAP所成的角的大小为
如图,四棱锥S-ABCD的底面是矩形,SA⊥底面ABCD,P为BC边的中点,AD=2,SA=AB=1.则PD与平面SAP所成的角的大小为