题目内容
若△ABC的三边为a,b,c,若f(x)=b2x2+(b2+c2-a2)x+c2,则y=f(x)的零点个数为 个.
考点:函数零点的判定定理
专题:计算题,函数的性质及应用
分析:函数的零点转化为方程解的个数判断,借助两边之和大于第三边.
解答:
解:f(x)=b2x2+(b2+c2-a2)x+c2的零点个数就是方程f(x)=0的解的个数;
∵△=(b2+c2-a2)2-4b2c2=(b2+2bc+c2-a2)(b2-2bc+c2-a2)
=(b+c-a)(b+c+a)(a+b-c)(b-c-a),
∵a,b,c为△ABC的三边长;
∴b+c-a>0,b+c+a>0,a+b-c>0,b-c-a<0;
则方程f(x)=0没有实根.
即y=f(x)的零点个数为0.
∵△=(b2+c2-a2)2-4b2c2=(b2+2bc+c2-a2)(b2-2bc+c2-a2)
=(b+c-a)(b+c+a)(a+b-c)(b-c-a),
∵a,b,c为△ABC的三边长;
∴b+c-a>0,b+c+a>0,a+b-c>0,b-c-a<0;
则方程f(x)=0没有实根.
即y=f(x)的零点个数为0.
点评:本题考查了函数零点与方程的根之间的关系,属于基础题.

练习册系列答案
相关题目
已知2x+y=2,则9x+3y的最小值为( )
A、2
| ||
| B、4 | ||
| C、12 | ||
| D、6 |
 如图,已知在200m高的山顶A处,测得山下一塔顶B与塔底C的俯角分别是30°,
如图,已知在200m高的山顶A处,测得山下一塔顶B与塔底C的俯角分别是30°,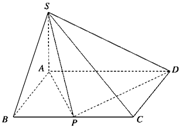 如图,四棱锥S-ABCD的底面是矩形,SA⊥底面ABCD,P为BC边的中点,AD=2,SA=AB=1.则PD与平面SAP所成的角的大小为
如图,四棱锥S-ABCD的底面是矩形,SA⊥底面ABCD,P为BC边的中点,AD=2,SA=AB=1.则PD与平面SAP所成的角的大小为