题目内容
将函数f(x)=sin(2x-
)的图象向右平移
个单位所得到的一条对称轴的方程是( )
| π |
| 6 |
| π |
| 3 |
A、x=
| ||
B、x=
| ||
C、x=
| ||
| D、x=π |
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:利用函数y=Asin(ωx+φ)的图象变换,可求得f(x-
)=sin(2x-
),利用正弦函数的对称性即可求得答案.
| π |
| 3 |
| 5π |
| 6 |
解答:
解:∵f(x)=sin(2x-
),
∴f(x-
)=sin[2(x-
)-
]=sin(2x-
),
其对称轴方程由2x-
=kπ-
(k∈Z)得:x=
+
(k∈Z),
显然,当k=0时,x=
就是该函数的一条对称轴的方程,
故选:C.
| π |
| 6 |
∴f(x-
| π |
| 3 |
| π |
| 3 |
| π |
| 6 |
| 5π |
| 6 |
其对称轴方程由2x-
| 5π |
| 6 |
| π |
| 2 |
| kπ |
| 2 |
| π |
| 6 |
显然,当k=0时,x=
| π |
| 6 |
故选:C.
点评:本题考查函数y=Asin(ωx+φ)的图象变换,突出考查正弦函数的对称性的应用,属于中档题.

练习册系列答案
相关题目
在一次抛硬币实验中,甲、乙两人各抛一枚硬币一次,设命题p是“甲抛的硬币正面向上”,q是“乙抛的硬币正面向上”,则命题“至少有一人抛的硬币是正面向下”可表示为( )
| A、(¬p)∨(¬q) |
| B、p∧(¬q) |
| C、(¬p)∧(¬q) |
| D、p∨q |
设x、y满足约束条件
,若z=x2+y2,则z的最小值为( )
|
A、
| ||
B、
| ||
C、
| ||
D、
|
阅读如图的程序框图,则输出的S等于( )


| A、-51 | B、50 |
| C、-50 | D、51 |
i是虚数单位.已知复数z=
,则复数Z对应点落在( )
| i-2 |
| 1-i |
| A、第四象限 | B、第三象限 |
| C、第二象限 | D、第一象限 |
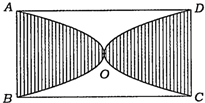 如图,矩形ABCD的面积为3,以矩形的中心O为顶点作两条抛物线,分别过点A、B和点C、D,若在矩形ABCD中随机撒入300颗豆子,则落在阴影部分内的豆子大约是
如图,矩形ABCD的面积为3,以矩形的中心O为顶点作两条抛物线,分别过点A、B和点C、D,若在矩形ABCD中随机撒入300颗豆子,则落在阴影部分内的豆子大约是