题目内容
19.为了考察某种中成药预防流感的效果,抽样调查40人,得到如下数据 | 患流感 | 未患流感 |
| 服用药 | 2 | 18 |
| 未服用药 | 8 | 12 |
| P(K2>k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | 0.05 | B. | 0.025 | C. | 0.01 | D. | 0.005 |
分析 根据表中数据,计算观测值K2,参考临界值即可得出结论;
解答 解:根据表中数据,计算观测值为
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$=$\frac{40{×(2×12-8×18)}^{2}}{10×30×20×20}$=4.8>3.84,
参考临界值得:认为“该药物有效”,该结论出错的概率不超过0.05.
故选:A.
点评 本题考查了独立性检验的应用问题,是基础题.

练习册系列答案
相关题目
10.曲线y=lgx在x=1处的切线斜率是( )
| A. | $\frac{1}{ln10}$ | B. | ln10 | C. | lne | D. | $\frac{1}{lne}$ |
12.用随机事件发生的频率去估算这个事件发生的概率.下列结论正确的是( )
| A. | 事件A发生的概率P(A)是0<P(A)<1 | |
| B. | 事件A发生的概率P(A)=0.999,则事件A是必然事件 | |
| C. | 用某种药物对患有胃溃疡的500名病人治疗,结果有380人有明显的疗效,现有胃溃疡的病人服用此药,则估计有明显疗效的可能性为76% | |
| D. | 某奖券中奖率为0.5,则某人购买此券10张,一定有5张中奖 |
13.若复数z=$\frac{2}{1-i}$(i是虚数单位),则|z|=( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
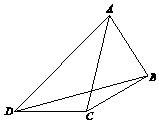 在如图所示的平面图形中,已知CD=$\sqrt{2}$,∠BCA=45°,∠ACD=105°,∠CDB=15°,∠BDA=30°.
在如图所示的平面图形中,已知CD=$\sqrt{2}$,∠BCA=45°,∠ACD=105°,∠CDB=15°,∠BDA=30°.