题目内容
5.下列说法正确的是( )| A. | 给定命题p、q,若p∧q是真命题,则¬p是假命题 | |
| B. | 两个三角形全等是这两个三角形面积相等的必要条件 | |
| C. | 命题“?x∈R,x2+x+2013>0”的否定是“?x∈R,x2+x+2013<0” | |
| D. | 函数f(x)=$\frac{1}{x}$在其定义域上是减函数 |
分析 根据p∧q,¬p的真假和p,q真假的关系,必要条件,充分条件的概念,命题的否命题,反比例函数的单调性,即可找出说法正确的选项.
解答 解:A.正确,若p∧q为真命题,则p是真命题,∴¬p是假命题;
B.不正确,若两个三角形全等,则这两个三角形面积相等,所以是充分条件;
C.不正确,命题“?x∈R,x2+x+2013>0”的否定是“?x∈R,x2+x+2013≤0”;
D.不正确,f(x)=$\frac{1}{x}$的定义域不连续,所以在定义域上不具有单调性.
故选A.
点评 考查反比例函数的单调性,充分条件,必要条件的概念,命题的否定,以及p∧q,¬p的真假和p,q真假的关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.设a、b为两条不同的直线,α为一个平面,下列命题中为真命题的是( )
| A. | 若a∥b,a∥α,则b∥α | B. | 若a⊥b,a∥α,则b⊥α | C. | 若a∥b,a⊥α,则b⊥α | D. | 若a⊥b,a⊥α,则b∥α |
20.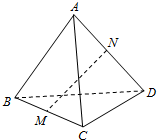 如图,在四面体ABCD,AB=CD,M,N分别是BC,AD的中点,若AB与CD所成的角的大小为60°,则MN和CD所成的角的大小为( )
如图,在四面体ABCD,AB=CD,M,N分别是BC,AD的中点,若AB与CD所成的角的大小为60°,则MN和CD所成的角的大小为( )
 如图,在四面体ABCD,AB=CD,M,N分别是BC,AD的中点,若AB与CD所成的角的大小为60°,则MN和CD所成的角的大小为( )
如图,在四面体ABCD,AB=CD,M,N分别是BC,AD的中点,若AB与CD所成的角的大小为60°,则MN和CD所成的角的大小为( )| A. | 30° | B. | 60° | C. | 30°或60° | D. | 15°或60° |
10.若平面α,β垂直,则下面可以作为这两个平面的法向量的是( )
| A. | $\overrightarrow{{n}_{1}}$=(1,2,1),$\overrightarrow{{n}_{2}}$=(-3,1,1) | B. | $\overrightarrow{{n}_{1}}$=(1,1,2),$\overrightarrow{{n}_{2}}$=(-2,1,1) | ||
| C. | $\overrightarrow{{n}_{1}}$=(1,1,1),$\overrightarrow{{n}_{2}}$=(-1,2,1) | D. | $\overrightarrow{{n}_{1}}$=(1,2,1),$\overrightarrow{{n}_{2}}$=(0,-2,-2) |
14.若p:a<1,q:关于x的二次方程x2+(a+1)x+a-2=0的一个根大于零,另一根小于零,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
 如图,已知线段AB在平面α内,线段AC⊥α,线段BD⊥AB,且AB=7,AC=BD=24,CD=25,求线段BD与平面α所成的角30°.
如图,已知线段AB在平面α内,线段AC⊥α,线段BD⊥AB,且AB=7,AC=BD=24,CD=25,求线段BD与平面α所成的角30°.