题目内容
已知等差数列{an}首项a1=1,公差为d,且数列{2 a n}是公比为4的等比数列,
(1)求d;
(2)求数列{an}的通项公式an及前n项和Sn;
(3)求数列{
}的前n项和Tn.
(1)求d;
(2)求数列{an}的通项公式an及前n项和Sn;
(3)求数列{
| 1 |
| an•an+1 |
考点:数列的求和,等比数列的通项公式
专题:综合题,等差数列与等比数列
分析:(1)利用数列{an}是公差为d的等差数列,数列{2an}是公比为4的等比数列,即可求d;
(2)利用等差数列的通项与求和公式,即可求数列{an}的通项公式an及前n项和Sn;
(3)利用裂项法求数列{
}的前n项和Tn.
(2)利用等差数列的通项与求和公式,即可求数列{an}的通项公式an及前n项和Sn;
(3)利用裂项法求数列{
| 1 |
| an•an+1 |
解答:
解:(1)∵数列{an}是公差为d的等差数列,数列{2an}是公比为4的等比数列,
∴
=2an+1-an=2d=4,求得d=2…(4分)
(2)由此知an=1+2(n-1)=2n-1,Sn=n2…(8分)
(3)令bn=
=
=
(
-
)…(10分)
则Tn=b 1+b2+b3+…+bn=
[(
-
)+(
-
)+(
-
)+…+(
-
)]=
(1-
)=
…(12分)
∴
| 2an+1 |
| 2an |
(2)由此知an=1+2(n-1)=2n-1,Sn=n2…(8分)
(3)令bn=
| 1 |
| an•an+1 |
| 1 |
| (2n-1)•(2n+1) |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
则Tn=b 1+b2+b3+…+bn=
| 1 |
| 2 |
| 1 |
| 1 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 7 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
| 1 |
| 2 |
| 1 |
| 2n+1 |
| n |
| 2n+1 |
点评:本题考查数列的求和,考查等差数列的通项公式,突出考查解方程组与裂项求和,属于中档题.

练习册系列答案
相关题目
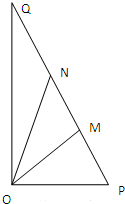 某房地产项目打造水景工程,拟在小区绿地中建设人工湖.该绿地形状为Rt△OPQ(如图),∠POQ=90°,OP=40m,OQ=40
某房地产项目打造水景工程,拟在小区绿地中建设人工湖.该绿地形状为Rt△OPQ(如图),∠POQ=90°,OP=40m,OQ=40