题目内容

过椭圆
x2
3
+y2=1的一个焦点F1的直线与椭圆交于A、B两点，则A、B与椭圆的另一焦点F2构成的△ABF2的周长为
 
．
考点：椭圆的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：把椭圆的方程化为标准方程，求出a的值，由△ABF2的周长是 （|AF1|+|AF2|）+（|BF1|+|BF2|）=2a+2a 求出结果．
解答： 解：∵椭圆
x2
3
+y2=1，
∴a=
3
，
故△ABF2的周长是 （|AF1|+|AF2|）+（|BF1|+|BF2|）
=2a+2a=4a=4
3
，
故答案为：4
3
．
点评：本题考查椭圆的定义、标准方程，以及简单性质的应用，利用椭圆的定义是解题的关键．
练习册系列答案
相关题目
设函数f（x）=
lnx
x
在区间（a，a+2）上单调递增，则a的取值范围为
 
．
设函数 f（x）对于任意的x，y∈R，都有f（x+y）=f（x）+f（y）且x＞0时f（x）＜0，f（1）=-2．
（1）判断f（x）的奇偶性，并证明．
（2）证明f（x）在R上是减函数，并求出x∈[-3，3]时，f（x）的最大值及最小值．
（3）若f（2x+5）+f（6-7x）＞4，求x的取值范围．
如图，在△ABC中，|
AB
|=3，|
AC
|=1，l为BC的垂直平分线且交BC于点D，E为l上异于D的任意一点，F为线段AD上的任意一点．
（1）求
AD
•（
AB
-
AC
）的值；
（2）判断
AE
•（
AB
-
AC
）的值是否为一常数，并说明理由；
（3）若AC⊥BC，求
AF
•（
FB
+
FC
）的最大值．
tan2010°=
 
．
设
OA
=（1，-2），
OB
=（a，-1），
OC
=（-b，0），（a＞0，b＞0，O为坐标原点），若A，B，C三点共线，则
1
a
+
2
b
的最小值是
 
．
在长方体ABCD-A1B1C1D1中，AD=AB=
2
，AA1=2，如图．
（1）当点P在BB1上运动时（点P∈BB1，且异于B，B1），设PA∩BA1=M，PC∩BC1=N，求证：MN∥平面ABCD．
（2）当点P是BB1的中点时，求异面直线PC与AD1所成角．
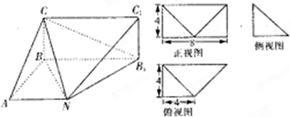已知某几何体的直观图和三视图如图所示，其正视图为矩形，侧视图为等腰直角三角表，俯视图为直角梯形．
（Ⅰ）求证：BN⊥平面C1B1N；
（Ⅱ）求直线C1N与平面CNB1所成角的正弦值．
函数f（x）=x2+2（a-1）x+2在区间[-1，4]上为减函数，则a的取值范围是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网