题目内容
13．在△ABC中，已知sinA：sinB：sinC=6：8：13，则△ABC是（ ）| A． | 钝角三角形 | B． | 锐角三角形 | C． | 直角三角形 | D． | 不能确定 |
分析 由正弦定理可知a：b；c=6：8：13，利用余弦定理求出最大角C的余弦判断C与90°的大小关系．
解答 解：△ABC中，∵sinA：sinB：sinC=6：8：13，
∴a：b；c=6：8：13．
不妨设a=6，b=8，c=13．
则cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=$\frac{36+64-169}{2×6×8}=-$$\frac{23}{32}$＜0．
∴C是钝角．
故选：A．
点评 本题考查了正弦定理，余弦定理，属于基础题．
练习册系列答案
相关题目
18．已知向量$\overrightarrow{AB}$=（2，0），$\overrightarrow{AC}$=（1，6），则（2$\overrightarrow{AB}$+3$\overrightarrow{CA}$）$•\overrightarrow{BC}$=（ ）
| A． | 109 | B． | 101 | C． | -107 | D． | -109 |
4．双曲线16x2-9y2=144的离心率为（ ）
| A． | $\frac{5}{3}$ | B． | $\frac{4}{3}$ | C． | $\frac{3}{4}$ | D． | $\frac{3}{5}$ |
8．已知命题p：存在x0＞0，使2${\;}^{{x}_{0}}$＜1，则￢p是（ ）
| A． | 对任意x＞0，都有2x≥1 | B． | 对任意x≤0，都有2x＜1 | ||
| C． | 存在x0＞0，使2${\;}^{{x}_{0}}$≥1 | D． | 存在x0≤0，使2${\;}^{{x}_{0}}$＜1 |
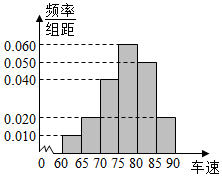2016年“双节”期间，高速公路车辆较多，某调查公司在一服务区从小型汽车中按进服务区的先后每间隔35辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查，将他们在某段高速公路的车速（km/h）分成六段：