Question

在△ABC中，∠C=90°，M是BC边上的点，且2|CM|=|MB|，若∠BAM=30°，则sin∠BAC=

 

．

Answer 1

考点：正弦定理

专题：三角函数的求值

分析：如图所示，设|BC|=a，|AC|=b，|AB|=a，根据2|CM|=|MB|，表示出|CM|=

1

3

a，|MB|=

2

3

a，在三角形ABM中，利用正弦定理表示出sin∠AMB，即为sin∠AMC，在直角三角形ACM中，利用诱导公式得到cos∠CAM=sin∠AMC，表示出cos∠CAM，再利用锐角三角函数定义表示出cos∠CAM，两者相等得到a=

3

b，再利用勾股定理表示出c，利用锐角三角函数定义即可求出sin∠BAC的值．

解答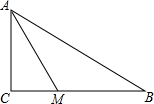： 解：如图所示，设|BC|=a，|AC|=b，|AB|=a，
∵2|CM|=|MB|，∴|CM|=

1

3

a，|MB|=

2

3

a，
在△ABM中，利用正弦定理得：

c

sin∠AMB

=

|MB|

sin∠BAM

，即

c

sin∠AMB

=

2 3 a

1 2

，
∴sin∠AMB=

3c

4a

，
∴cos∠CAM=cos（

π

2

-∠AMC）=sin∠AMC=sin∠AMB=

3c

4a

，
在Rt△ACM中，cos∠CAM=

|AC|

|AM|

=

b

b2+( 1 3 a)2

，
可得

3c

4a

=

b

b2+( 1 3 a)2

，
两边平方得：

9c2

16a2

=

9(a2+b2)

16a2

=

b2

b2+ 1 9 a2

，
整理得：（a²-3b²）²=0，即a²=3b²，
∴a=

3

b，
再由a²+b²=c²，得到c=2b，
则sin∠CAB=

a

c

=

3 b

2b

=

3

2

．

点评：此题考查了正弦定理，锐角三角函数定义，同角三角函数间的基本关系，以及特殊角的三角函数值，熟练掌握定理是解本题的关键．