题目内容
已知函数f（x）=
|
（1）在直角坐标系中画出f（x）的图象；
（2）若f（x）=5，求x值；
（3）用单调性定义证明函数f（x）在区间[2，+∞）上单调递增．
考点：函数单调性的判断与证明,分段函数的应用
专题：函数的性质及应用
分析：（1）根据函数f（x）的分段情况，在同一坐标系中画出函数y=f（x）的图象；
（2）由函数y=f（x）的图象知，x≥2时，y=f（x）=5，求出x的值；
（3）用单调性的定义证明函数的单调性，步骤是取值，作差，判正负，下结论．
（2）由函数y=f（x）的图象知，x≥2时，y=f（x）=5，求出x的值；
（3）用单调性的定义证明函数的单调性，步骤是取值，作差，判正负，下结论．
解答：
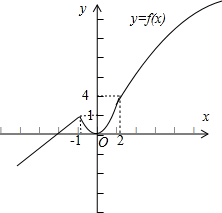解：（1）当x＜-1时，y=f（x）=x+2，
当-1≤x≤2时，y=f（x）=x2，
当x≥2时，y=f（x）=x+
，
∴画出函数y=f（x）的图象，如图；
（2）由函数y=f（x）的图象知，
x≥2时，y=f（x）=x+
=5，
解得x=4；
（3）证明：任取x1，x2∈[2，+∞），且x1＜x2；
∴f（x1）-f（x2）=（x1+
）-（x2+
）=
，
∵2≤x1＜x2，∴x1-x2＜0，x1x2-4＞0，
∴f（x1）-f（x2）＜0，
即f（x1）＜f（x2）；
∴f（x）是区间[2，+∞）上的增函数．
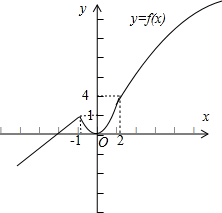解：（1）当x＜-1时，y=f（x）=x+2，当-1≤x≤2时，y=f（x）=x2，
当x≥2时，y=f（x）=x+
| 4 |
| x |
∴画出函数y=f（x）的图象，如图；
（2）由函数y=f（x）的图象知，
x≥2时，y=f（x）=x+
| 4 |
| x |
解得x=4；
（3）证明：任取x1，x2∈[2，+∞），且x1＜x2；
∴f（x1）-f（x2）=（x1+
| 4 |
| x1 |
| 4 |
| x2 |
| (x1-x2)(x1x2-4) |
| x1x2 |
∵2≤x1＜x2，∴x1-x2＜0，x1x2-4＞0，
∴f（x1）-f（x2）＜0，
即f（x1）＜f（x2）；
∴f（x）是区间[2，+∞）上的增函数．
点评：本题考查了分段函数的解析式以及图象的应用问题，也考查了用定义来证明函数的单调性问题，是综合性题目．
练习册系列答案
相关题目
椭圆C：
+
=1的长轴长和准线方程分别为（ ）
| x2 |
| 16 |
| y2 |
| 7 |
A、4，x=±
| ||
B、8，x=±
| ||
C、4，x=±
| ||
D、8，x=±
|
函数f（x）=3x-9的零点是（ ）
| A、（2，0） | B、（3，0） |
| C、2 | D、3 |