题目内容
已知f(x)=2+logax(1≤x≤9),其中a满足
<-a2+7a-10(a∈N)求函数y=2f(x2)-[f(x)-
]2的最大值.
| 4 | (a-2)4 |
| 3 |
| 2 |
考点:函数的最值及其几何意义
专题:函数的性质及应用
分析:利用不等式求出a的范围,利用函数的表达式化简为log3x的二次函数,求出新函数的定义域,然后求解最大值.
解答:
解:由
<-a2+7a-10得:
|a-2|<-a2+7a-10,
⇒
或者
解得2<a<4,
又a∈N,∴a=3.f(x)=2+log3x(1≤x≤9),…(4分)y=2f(x2)-[f(x)-
]2=2(2+2log3x)-[log3x+
]2
=-(log3x)2+3log3x+
=-(log3x-
)2+6…(8分)
又∵f(x)的定义域为[1,9],
∴要使函数y=2f(x2)-[f(x)-
]2)有意义,
必须有
∴1≤x≤3,∴0≤log3x≤1.
故当log3x=0,即x=1时,y的最大值为
;
当log3x=1,即x=3时,y的最大值为
.…(12分)
| 4 | (a-2)4 |
|a-2|<-a2+7a-10,
⇒
|
|
解得2<a<4,
又a∈N,∴a=3.f(x)=2+log3x(1≤x≤9),…(4分)y=2f(x2)-[f(x)-
| 3 |
| 2 |
| 1 |
| 2 |
=-(log3x)2+3log3x+
| 15 |
| 4 |
| 3 |
| 2 |
又∵f(x)的定义域为[1,9],
∴要使函数y=2f(x2)-[f(x)-
| 3 |
| 2 |
必须有
|
故当log3x=0,即x=1时,y的最大值为
| 15 |
| 4 |
当log3x=1,即x=3时,y的最大值为
| 23 |
| 4 |
点评:本题考查不等式的解法函数的最值的求法,二次函数的性质的综合应用,考查转化思想以及计算能力.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
将函数y=sinx+cosx(x∈R)的图象向左平移m(m>0)个单位长度后,得到图象关于y轴对称,则m的最小值为( )
A、
| ||
B、
| ||
C、
| ||
| D、π |
已知f(x)=
,则下列函数的图象错误的是( )
|
A、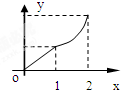 f(x-1)的图象 |
B、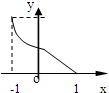 f(-x)的图象 |
C、 f(|x|)的图象 |
D、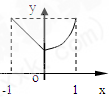 |f(x)|的图象 |
下列函数中,与函数y=x相同的函数是( )
| A、y=|x| | ||
B、y=
| ||
C、y=(
| ||
| D、y=logaax(a>0,且a≠1) |