题目内容
若定义在R上的函数f(x)满足f(-x)+f(x)=0,且f(x+1)=f(1-x),若f(1)=5,则f(2015)=( )
| A、5 | B、-5 | C、0 | D、3 |
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:由题意求出函数的周期,转化f(2015)为已知函数定义域内的自变量,然后求值.
解答:
解:∵定义在R上的函数f(x)满足f(-x)+f(x)=0,
∴f(-x)=-f(x),
∵f(x+1)=f(1-x),
∴f(x+2)=f[(x+1)+1]=f[1-(x+1)]=f(-x)=-f(x),
即f(x+2)=-f(x),
f(x+4)=-f(x+2),
∴f(x+4)=f(x),
∴函数的周期为4,
∴f(2015)=f(4×504-1)=f(-1)=-f(1),
∵f(1)=5,
∴f(2015)=-5.
故选:B.
∴f(-x)=-f(x),
∵f(x+1)=f(1-x),
∴f(x+2)=f[(x+1)+1]=f[1-(x+1)]=f(-x)=-f(x),
即f(x+2)=-f(x),
f(x+4)=-f(x+2),
∴f(x+4)=f(x),
∴函数的周期为4,
∴f(2015)=f(4×504-1)=f(-1)=-f(1),
∵f(1)=5,
∴f(2015)=-5.
故选:B.
点评:本题考查函数的奇偶性、周期性的应用,函数值的求法,考查计算能力.本题难度不大,属于基础题.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
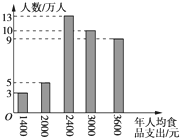 对“小康县”的经济评价标准:
对“小康县”的经济评价标准:①年人均收入不小于7000元;
②年人均食品支出不大于收入的35%.某县有40万人,调查数据如下:
| 年人均收入/元 | 0 | 2000 | 4000 | 6000 | 8000 | 10 000 | 12 000 | 16 000 |
| 人数/万人 | 6 | 3 | 5 | 5 | 6 | 7 | 5 | 3 |
| A、是小康县 |
| B、达到标准①,未达到标准②,不是小康县 |
| C、达到标准②,未达到标准①,不是小康县 |
| D、两个标准都未达到,不是小康县 |
下列各式中最小值为2的是( )
A、sinx+
| ||||
B、
| ||||
| C、ex+e-x(x∈R) | ||||
D、x+
|
已知集合A=[x|-1≤x<2},B={x|x-a≤0},若A⊆B,则实数a的取值范围是( )
| A、a≤2 | B、a≥-1 |
| C、a>-1 | D、a≥2 |
已知等比数列{an}的公比q=-
,则
等于( )
| 1 |
| 3 |
| a1+a3+a5 |
| a2+a4+a6 |
A、-
| ||
| B、-3 | ||
C、
| ||
| D、3 |
方程lg(lnx)=0的解为x等于( )
| A、1 | B、e | C、10 | D、π |