题目内容
将函数y=sinx+cosx(x∈R)的图象向左平移m(m>0)个单位长度后,得到图象关于y轴对称,则m的最小值为( )
A、
| ||
B、
| ||
C、
| ||
| D、π |
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:首先把函数转化成正弦型函数,进一步利用平移变换得到f(x)=
sin(x+m+
)再利用图象关于y轴对称得到结果.
| 2 |
| π |
| 4 |
解答:
解:函数y=sinx+cosx=
sin(x+
)(x∈R)的图象向左平移m(m>0)个单位长度后,
得到:f(x)=
sin(x+m+
)得到图象关于y轴对称,
所以:m+
=kπ+
(k∈Z),
解得:m=kπ+
,
当k=0时m=
,
故选:A.
| 2 |
| π |
| 4 |
得到:f(x)=
| 2 |
| π |
| 4 |
所以:m+
| π |
| 4 |
| π |
| 2 |
解得:m=kπ+
| π |
| 4 |
当k=0时m=
| π |
| 4 |
故选:A.
点评:本题考查的知识要点:函数图象的变换符合左加右减的性质,正弦型函数的图象关于y轴对称符合的等量关系.

练习册系列答案
相关题目
若3a>1,则实数a的取值范围为( )
| A、a<0 | B、0<a<1 |
| C、a>0 | D、a>2 |
四面体ABCD的四个顶点都在球O的表面上,AB⊥平面BCD,△BCD是边长为3的等边三角形.若AB=2,则球O的表面积为( )
| A、4π | B、12π |
| C、16π | D、32π |
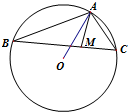 如图所示,O为△ABC的外接圆圆心,AB=10,AC=4,∠BAC为钝角,M是边BC的点,且满足
如图所示,O为△ABC的外接圆圆心,AB=10,AC=4,∠BAC为钝角,M是边BC的点,且满足| BM |
| MC |
| AM |
| AO |
| A、21 | B、22 | C、29 | D、36 |
将长为1的小棒随机拆成3小段,则这3小段能构成三角形的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|