题目内容
 四棱锥P-ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,在侧面PBC内有BE⊥PC于E,且BE=
四棱锥P-ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,在侧面PBC内有BE⊥PC于E,且BE=
| ||
| 3 |
(1)试在AB上找一点F,使EF∥平面PAD.
(2)在平面PAD上是否存在一点G,使GE⊥PBC.
考点:直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)过E作EG∥CD交PD于G,连接AG,在AB上取点F,使AF=EG,要证明EF∥平面PAD,只需证明FE∥AG即可;然后确定F的位置;
(2)由P向AH作垂线交AD于I,在△PIC中过E作PC的垂线交PI于G点,则EG⊥PC,利用线面垂直的判定定理PI⊥平面AHEB,进而可知PI⊥BE,进而根据BE⊥PC由线面垂直的判定证明出BE⊥平面PIC,进而证明出平面PBC⊥平面PIC,最后根据面面垂直的性质证明出GE⊥PBC.
(2)由P向AH作垂线交AD于I,在△PIC中过E作PC的垂线交PI于G点,则EG⊥PC,利用线面垂直的判定定理PI⊥平面AHEB,进而可知PI⊥BE,进而根据BE⊥PC由线面垂直的判定证明出BE⊥平面PIC,进而证明出平面PBC⊥平面PIC,最后根据面面垂直的性质证明出GE⊥PBC.
解答:
解:(1)在平面PCD内,过E作EH∥CD交PD于H,连接AH,在AB上取点F,使AF=EH,则F即为所求作的点.
∵EH∥CD∥AF,EH=AF,
∴四边形FEHA为平行四边形,
∴FE∥AH.
又AH?平面PAD,FE?平面PAD,
∴EF∥平面PAD.
又在Rt△BCE中,CE=
=
a.
在Rt△PBC中,BC2=CE•CP
∴CP=
a.
又
=
,
∴EH=
•CD=
a,
∴AF=EH=
a.
∴点F为AB的一个三等分点.
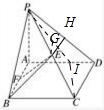
(2)存在,
由P向AH作垂线交AD于I,在△PIC中过E作PC的垂线交PI于G点,则EG⊥PC,
证明如下;
∵PA⊥AB,AD⊥AB,
∴AB⊥平面PAD,
∵PI?平面PAD,
∴AB⊥PI,
∵PI⊥AH,AH?平面AHEB,AB?平面AHEB,AB∩AH=A,
∴PI⊥平面AHEB,
∵BE?平面AHEB,
∴PI⊥BE,
∵BE⊥PC,PC?平面PIC,PI?平面PIC,PC∩PI=P,
∴BE⊥平面PIC,
∵BE?平面PBC,
∴平面PBC⊥平面PIC,
∵平面PBC∩平面PIC=PC,BG⊥PC,
∴BG⊥平面PBC.
∵EH∥CD∥AF,EH=AF,
∴四边形FEHA为平行四边形,
∴FE∥AH.
又AH?平面PAD,FE?平面PAD,
∴EF∥平面PAD.
又在Rt△BCE中,CE=
| BC2-BE2 |
| ||
| 3 |
在Rt△PBC中,BC2=CE•CP
∴CP=
| 3 |
又
| EH |
| CD |
| PE |
| PC |
∴EH=
| PE |
| PC |
| 2 |
| 3 |
∴AF=EH=
| 2 |
| 3 |
∴点F为AB的一个三等分点.

(2)存在,
由P向AH作垂线交AD于I,在△PIC中过E作PC的垂线交PI于G点,则EG⊥PC,
证明如下;
∵PA⊥AB,AD⊥AB,
∴AB⊥平面PAD,
∵PI?平面PAD,
∴AB⊥PI,
∵PI⊥AH,AH?平面AHEB,AB?平面AHEB,AB∩AH=A,
∴PI⊥平面AHEB,
∵BE?平面AHEB,
∴PI⊥BE,
∵BE⊥PC,PC?平面PIC,PI?平面PIC,PC∩PI=P,
∴BE⊥平面PIC,
∵BE?平面PBC,
∴平面PBC⊥平面PIC,
∵平面PBC∩平面PIC=PC,BG⊥PC,
∴BG⊥平面PBC.
点评:本题考查直线与平面平行的判定,直线与平面垂直的判定.考查学生的逻辑思维能力和空间观察能力.第二问中作出与平面PBC垂直的面PIC时解题的关键,往常需要作出与面垂直的辅助线,这次需作出与之垂直的面,难度较大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在极坐标系中,圆C:ρ=2
sin(θ+
)上到直线l:ρcosθ=2距离为1的点的个数为( )
| 2 |
| π |
| 4 |
| A、1 | B、2 | C、3 | D、4 |
 已知函数f(x)=
已知函数f(x)=