题目内容
12.已知a1=2,an≠0,且an+1-an=2an+1an,求an.分析 根据数列的递推关系推出新数列是等差数列,然后求解数列的通项公式即可.
解答 解:∵2an+1an=an+1-an,
∴$\frac{1}{{a}_{n}}-\frac{1}{{a}_{n+1}}=2$,
∵a1=2,
∴$\frac{1}{{a}_{1}}$=$\frac{1}{2}$,∴$\{\frac{1}{{a}_{n}}\}$是等差数列,首项为$\frac{1}{2}$,公差为:-2,∴$\frac{1}{{a}_{n}}=\frac{1}{2}+(n-1)(-2)$=$\frac{-4n+5}{2}$,
∴an=$\frac{2}{5-4n}$,
故答案为:$\frac{2}{5-4n}$.
点评 本题主要考查数列通项公式的求解,根据递推关系是解决本题的关键.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
3.已知直线l1:3x+4y=0和l2:3x-4y=0的倾斜角( )
| A. | 互补 | B. | 互余 | C. | 相等 | D. | 互为相反数 |
7.某公司生产一种产品,固定成本为20 000元,每生产一单位的产品,成本增加100元,若总收入R与年产量x(0≤x≤390)的关系是$R(x)=-\frac{x^3}{9000}+400x,0≤x≤390$,则当总利润最大时,每年生产的产品单位数是( )
| A. | 300 | B. | 250 | C. | 200 | D. | 100 |
17.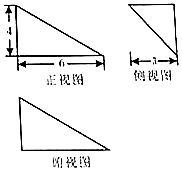 某几何体的三视图如图.若该几何体的顶点都在球O的表面上,则球O的体积是( )
某几何体的三视图如图.若该几何体的顶点都在球O的表面上,则球O的体积是( )
 某几何体的三视图如图.若该几何体的顶点都在球O的表面上,则球O的体积是( )
某几何体的三视图如图.若该几何体的顶点都在球O的表面上,则球O的体积是( )| A. | $\frac{\sqrt{61}}{6}$π | B. | $\frac{\sqrt{61}}{24}$π | C. | $\frac{61\sqrt{61}}{2}$π | D. | $\frac{61\sqrt{61}}{6}$π |
4.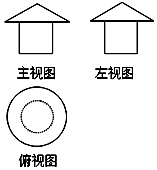 如图是一个空间几何体的三视图,其中主视图上半部分是一个底面边长为4、高为1的等腰三角形,主视图下半部分是一个边长为2的正方形,则该空间几何体的体积是( )
如图是一个空间几何体的三视图,其中主视图上半部分是一个底面边长为4、高为1的等腰三角形,主视图下半部分是一个边长为2的正方形,则该空间几何体的体积是( )
 如图是一个空间几何体的三视图,其中主视图上半部分是一个底面边长为4、高为1的等腰三角形,主视图下半部分是一个边长为2的正方形,则该空间几何体的体积是( )
如图是一个空间几何体的三视图,其中主视图上半部分是一个底面边长为4、高为1的等腰三角形,主视图下半部分是一个边长为2的正方形,则该空间几何体的体积是( )| A. | $(8+2\sqrt{5})π$ | B. | $\frac{10π}{3}$ | C. | $(10+2\sqrt{5})π$ | D. | $\frac{8π}{3}$ |