题目内容
19.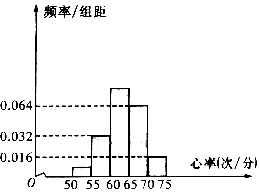 某学校的特长班有50名学生,其中有体育生20人,艺术生30名,在学校组织的一次体检中,该班所有学生进行了心率测试,心率全部介于50次/分到75次/分之间,现将数据分成五组,第一组[50,55),第二组[55,60),…,第五组[70,75),按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前三组的频率之比为a:4:10.
某学校的特长班有50名学生,其中有体育生20人,艺术生30名,在学校组织的一次体检中,该班所有学生进行了心率测试,心率全部介于50次/分到75次/分之间,现将数据分成五组,第一组[50,55),第二组[55,60),…,第五组[70,75),按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前三组的频率之比为a:4:10.(1)求a的值,并求这50名学生心率的平均数;
(2)因为学习专业的原因,体育生常年进行系统的身体锻炼,艺术生则很少进行系统的身体锻炼,若从第一组和第二组的学生中随机抽取一名,该学生是体育生的概率为0.8,请将下面的列联表补充完整,并判断是否有99.5%的把握认为心率小于60次/分与常年进行系统的身体锻炼有关?请说明理由.
参考数据:
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| 心率小于60次/分 | 心率不小于60次/分 | 合计 | |
| 体育生 | 8 | 12 | 20 |
| 艺术生 | 2 | 28 | 30 |
| 合计 | 10 | 40 | 50 |
分析 (1)求出各组的频数,即可求a的值,可得这50名学生心率的平均数.
(2)由(1)知,第一组和第二组的学生共10名,从而体育考生有10×0.8=8名,求出K2,与临界值比较,即可得出结论.
解答 解:(1)因为第二组数据的频率为 0.032×5=0.16,故第二组的频数为0.16×50=8,
第一组的频数为2a,第三组的频数为20,第四组的频数为16,第五组的频数为4
所以 2a=50-20-16-8-4=2⇒a=1;
这50名学生心率的平均数为$52.5×\frac{2}{50}+57.5×\frac{8}{50}$+$62.5×\frac{20}{50}$+$67.5×\frac{16}{50}+72.5×\frac{4}{50}$=63.7;
(2)由(1)知,第一组和第二组的学生共10名,从而体育考生有10×0.8=8名,
| 心率小于60次/分 | 心率不小于60次/分 | 合计 | |
| 体育生 | 8 | 12 | 20 |
| 艺术生 | 2 | 28 | 30 |
| 合计 | 10 | 40 | 50 |
∴有99.5%的把握认为心率小于60次/分与常年进行系统的身体锻炼有关.
点评 本题考查频率分布直方图,考查独立性检验知识的运用,属于中档题.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
7.已知变量x,y满足约束条件$\left\{\begin{array}{l}{x+y<0}\\{x-y<0}\\{x+2>0}\end{array}\right.$,则$\frac{y+1}{x}$的取值范围为( )
| A. | (-$\frac{3}{2}$,$\frac{1}{2}$] | B. | (-∞,$\frac{1}{2}$] | C. | (-$\frac{3}{2}$,$\frac{1}{2}$) | D. | (-∞,$\frac{1}{2}$) |
14.南北朝时期我国数学著作《张丘建算经》有一道题为:“今有十等人,每等一人,宫赐金以等次差降之,上三人先入,的金四斤,持出,下四人后入得金三斤,持出,中间三人未到者,亦依等次更给,问各得金几何?”则在该问题中,等级较高的二等人所得黄金比等级较低的八等人和九等人两人所得黄金之和( )
| A. | 多$\frac{7}{12}$斤 | B. | 少$\frac{7}{12}$斤 | C. | 多$\frac{1}{6}$斤 | D. | 少$\frac{1}{6}$斤 |
11.继共享单车之后,又一种新型的出行方式------“共享汽车”也开始亮相北上广深等十余大中城市,一款叫“一度用车”的共享汽车在广州提供的车型是“奇瑞eQ”,每次租车收费按行驶里程加用车时间,标准是“1元/公里+0.1元/分钟”,李先生家离上班地点10公里,每天租用共享汽车上下班,由于堵车因素,每次路上开车花费的时间是一个随机变量,根据一段时间统计40次路上开车花费时间在各时间段内的情况如下:
以各时间段发生的频率视为概率,假设每次路上开车花费的时间视为用车时间,范围为[15,65]分钟.
(Ⅰ)若李先生上、下班时租用一次共享汽车路上开车不超过45分钟,便是所有可选择的交通工具中的一次最优选择,设ξ是4次使用共享汽车中最优选择的次数,求ξ的分布列和期望.
(Ⅱ)若李先生每天上下班使用共享汽车2次,一个月(以20天计算)平均用车费用大约是多少(同一时段,用该区间的中点值作代表).
| 时间(分钟) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65] |
| 次数 | 8 | 14 | 8 | 8 | 2 |
(Ⅰ)若李先生上、下班时租用一次共享汽车路上开车不超过45分钟,便是所有可选择的交通工具中的一次最优选择,设ξ是4次使用共享汽车中最优选择的次数,求ξ的分布列和期望.
(Ⅱ)若李先生每天上下班使用共享汽车2次,一个月(以20天计算)平均用车费用大约是多少(同一时段,用该区间的中点值作代表).
9.从1,2,3,4四个数字中任取两个不同数字,则这两个数字之积小于5的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
 如图,四边形ABCD是边长为1的正方形,ED⊥平面ABCD,FB⊥平面ABCD,且ED=FB=1,M为BC的中点,N为AF的中点.
如图,四边形ABCD是边长为1的正方形,ED⊥平面ABCD,FB⊥平面ABCD,且ED=FB=1,M为BC的中点,N为AF的中点.