题目内容
9.已知双曲线${C_1}:\frac{x^2}{6}-\frac{y^2}{2}=1$与双曲线${C_2}:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的离心率相同,且双曲线C2的左、右焦点分别为F1,F2,M是双曲线C2一条渐近线上的某一点,且OM⊥MF2,${S_{△OM{F_2}}}=8\sqrt{3}$,则双曲线C2的实轴长为( )| A. | 4 | B. | $4\sqrt{3}$ | C. | 8 | D. | $8\sqrt{3}$ |
分析 根据条件先求出双曲线的离心率,然后利用a,b,c的关系求出渐近线的方程,结合三角形的面积公式进行求解即可.
解答 解:双曲线${C_1}:\frac{x^2}{6}-\frac{y^2}{2}=1$中,a1=$\sqrt{6}$,c1=$\sqrt{6+2}$=2$\sqrt{2}$,则离心率e=$\frac{2\sqrt{2}}{\sqrt{6}}$=$\frac{2\sqrt{3}}{3}$=$\frac{c}{a}$,
即c=$\frac{2\sqrt{3}}{3}$a,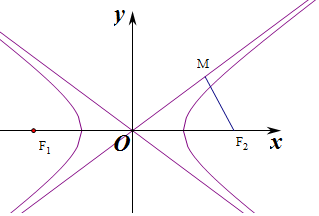 则b2=c2-a2=$\frac{1}{3}$a2,得b=$\frac{\sqrt{3}}{3}$a,即$\frac{b}{a}$=$\frac{\sqrt{3}}{3}$,
则b2=c2-a2=$\frac{1}{3}$a2,得b=$\frac{\sqrt{3}}{3}$a,即$\frac{b}{a}$=$\frac{\sqrt{3}}{3}$,
设双曲线的渐近线为y=$\frac{b}{a}$x,即bx-ay=0,
则右焦点F2,
∵OM⊥MF2,
∴MF2=$\frac{|bc|}{\sqrt{{a}^{2}+{b}^{2}}}$=$\frac{bc}{c}=b$,
则渐近线y=$\frac{b}{a}$x=$\frac{\sqrt{3}}{3}$x,则渐近线的倾斜角∠MOF2=30°,∠OF2M=60°,
则OF2=2MF2,即c=2b,
则三角形的面积${S_{△OM{F_2}}}=8\sqrt{3}$=$\frac{1}{2}$OF2MF2sin60°=$\frac{1}{2}$×b•2b•$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{2}$b2,
则b2=16,则a2=3b2=48,则a=4$\sqrt{3}$,
则2a=$8\sqrt{3}$,
即双曲线C2的实轴长为$8\sqrt{3}$,
故选:D.
点评 本题主要考查双曲线性质的应用,根据双曲线离心率,渐近线以及三角形的面积建立方程关系是解决本题的关键.

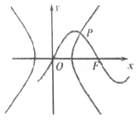 如图所示,已知函数y=$\sqrt{2}$sin$\frac{π}{4}$x经过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点F,函数y=$\sqrt{2}$sin$\frac{π}{4}$x与双曲线在第一象限交点为P,P的横坐标为3,则双曲线的渐近线方程为( )
如图所示,已知函数y=$\sqrt{2}$sin$\frac{π}{4}$x经过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点F,函数y=$\sqrt{2}$sin$\frac{π}{4}$x与双曲线在第一象限交点为P,P的横坐标为3,则双曲线的渐近线方程为( )| A. | x±y=0 | B. | x±2y=0 | C. | x±$\sqrt{3}$y=0 | D. | 2x±y=0 |
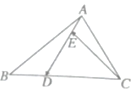 如图,在△ABC中,点D在BC边上,且CD=2DB,点E在AD边上,且AD=3AE,则用向量$\overrightarrow{AB},\overrightarrow{AC}$表示$\overrightarrow{CE}$为( )
如图,在△ABC中,点D在BC边上,且CD=2DB,点E在AD边上,且AD=3AE,则用向量$\overrightarrow{AB},\overrightarrow{AC}$表示$\overrightarrow{CE}$为( )| A. | $\overrightarrow{CE}=\frac{2}{9}\overrightarrow{AB}+\frac{8}{9}\overrightarrow{AC}$ | B. | $\overrightarrow{CE}=\frac{2}{9}\overrightarrow{AB}-\frac{8}{9}\overrightarrow{AC}$ | C. | $\overrightarrow{CE}=\frac{2}{9}\overrightarrow{AB}+\frac{7}{9}\overrightarrow{AC}$ | D. | $\overrightarrow{CE}=\frac{2}{9}\overrightarrow{AB}-\frac{7}{9}\overrightarrow{AC}$ |