题目内容
8.已知焦点在x轴上,离心率为$\frac{{\sqrt{6}}}{3}$的椭圆C的一个顶点是(0,1).(Ⅰ)求椭圆C的标准方程;
(Ⅱ)设直线l与椭圆C交于A、B两点,且OA⊥OB,O为坐标原点,判断直线l与圆x2+y2=1的位置关系?证明你的结论.
分析 (1)根据题意,设椭圆方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,椭圆的半焦距为c,结合题意可得$\left\{\begin{array}{l}\frac{c}{a}=\frac{{\sqrt{6}}}{3}\\ b=1\\{a^2}={b^2}+{c^2}\end{array}\right.$,解可得a、b的值,代入椭圆的方程即可得答案;
(2)根据题意,分析直线的斜率,分2种情况证明:①当直线l与x轴垂直时,由椭圆的对称性分析易得证明,②当直线l与x轴不垂直时,设l的方程为y=kx+m,联立直线与椭圆的方程,得到(3k2+1)x2+6kmx+3m2-3=0,结合根与系数的关系以及向量数量积的定义分析,可得证明;综合可得结论.
解答 解:(Ⅰ)依题意,设椭圆方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,设椭圆的半焦距为c,
又$\left\{\begin{array}{l}\frac{c}{a}=\frac{{\sqrt{6}}}{3}\\ b=1\\{a^2}={b^2}+{c^2}\end{array}\right.$,
所以$a=\sqrt{3},b=1,c=\sqrt{2}$.
所以椭圆C的方程为$\frac{x^2}{3}+{y^2}=1$.
(Ⅱ)直线l与圆x2+y2=1相交,
分2种情况证明:
①当直线l与x轴垂直时,由OA⊥OB及椭圆的对称性得直线l的方程为$x=±\frac{{\sqrt{3}}}{2}$,
此时l与圆x2+y2=1相交.
②当直线l与x轴不垂直时,
设l的方程为y=kx+m,
由$\left\{{\begin{array}{l}{y=kx+m}\\{\frac{x^2}{3}+{y^2}=1}\end{array}}\right.$,得到(3k2+1)x2+6kmx+3m2-3=0,
所以${x_1}+{x_2}=-\frac{6km}{{3{k^2}+1}}$,${x_1}{x_2}=\frac{{3{m^2}-3}}{{3{k^2}+1}}$,
于是$\overrightarrow{OA}•\overrightarrow{OB}={x_1}{x_2}+{y_1}{y_2}={x_1}{x_2}+({k{x_1}+m})({k{x_2}+m})=({{k^2}+1}){x_1}{x_2}+mk({{x_1}+{x_2}})+{m^2}$
=$({{k^2}+1})•\frac{{3{m^2}-3}}{{3{k^2}+1}}+mk({-\frac{6km}{{3{k^2}+1}}})+{m^2}$=$\frac{{({{k^2}+1})({3{m^2}-3})-6{k^2}{m^2}+{m^2}({3{k^2}+1})}}{{3{k^2}+1}}$
=$\frac{{3({{k^2}+1}){m^2}-3({{k^2}+1})-6{k^2}{m^2}+{m^2}({3{k^2}+1})}}{{3{k^2}+1}}=\frac{{4{m^2}-3({{k^2}+1})}}{{3{k^2}+1}}=0$,
所以${m^2}=\frac{{3({{k^2}+1})}}{4}$,此时△>0.
此时点O到直线l的距离$d=\frac{|m|}{{\sqrt{1+{k^2}}}}=\sqrt{\frac{{\frac{{3({{k^2}+1})}}{4}}}{{{k^2}+1}}}=\frac{{\sqrt{3}}}{2}<1$,
于是l与圆x2+y2=1相交.
点评 本题考查椭圆的几何性质,涉及直线与椭圆的位置关系,注意要分析直线的斜率是否存在.

| 时间 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期日 |
| 车流量x(万辆) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| PM2.5的浓度y(微克/立方米) | 28 | 30 | 35 | 41 | 49 | 56 | 62 |
(2)(I)利用(1)所求的回归方程,预测该市车流量为12万辆时PM2.5的浓度;(II)规定:当一天内PM2.5的浓度平均值在(0,50]内,空气质量等级为优;当一天内PM2.5的浓度平均值在(50,100]内,空气质量等级为良,为使该市某日空气质量为优或者为良,则应控制当天车流量不超过多少万辆?(结果以万辆为单位,保留整数)参考公式:回归直线的方程是$\widehaty=\widehatbx+\widehata$,其中$\widehatb=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x•\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}$,$\widehata=\overline y-\widehatb\overline x$.
| A. | {x|-2<x<2} | B. | {x|x<-2或x>2} | C. | {x|x<-2或2<x≤4} | D. | {x|x<-2或2<x<4} |
| A. | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1 | B. | $\frac{{x}^{2}}{32}$+$\frac{{y}^{2}}{16}$=1 | C. | $\frac{{x}^{2}}{36}$+$\frac{{y}^{2}}{20}$=1 | D. | $\frac{{x}^{2}}{20}$+$\frac{{y}^{2}}{4}$=1 |
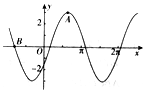 已知函数f(x)=Msin(ωx+φ)(M>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,其中A(2,3)(点A为图象的一个最高点),B(-$\frac{5}{2}$,0),则函数f(x)=3sin($\frac{π}{3}$x-$\frac{π}{6}$).
已知函数f(x)=Msin(ωx+φ)(M>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,其中A(2,3)(点A为图象的一个最高点),B(-$\frac{5}{2}$,0),则函数f(x)=3sin($\frac{π}{3}$x-$\frac{π}{6}$). 如图,四边形ABCD是边长为1的正方形,ED⊥平面ABCD,FB⊥平面ABCD,且ED=FB=1,M为BC的中点,N为AF的中点.
如图,四边形ABCD是边长为1的正方形,ED⊥平面ABCD,FB⊥平面ABCD,且ED=FB=1,M为BC的中点,N为AF的中点.