题目内容
18.已知命题p:不等式x2-(2m-1)x+m2≥0对任意实数x恒成立,命题q:m<1.(1)若p为真,求实数m的取值范围;
(2)若“p∧q”为假,“p∨q”为真,求实数m的取值范围.
分析 (1)根据二次函数的性质求出m的范围即可;(2)根据p与q为一真一假,得到关于m的不等式组,解出即可.
解答 解:(1)不等式x2-(2m-1)x+m2≥0对任意实数x恒成立,
则△=(2m-1)2-4m2=-4m+1≤0得:m≥$\frac{1}{4}$;
(2)若“p∧q”为假,“p∨q”为真,
则p与q为一真一假,
①当p真q假时,$\left\{\begin{array}{l}{m≥\frac{1}{4}}\\{m≥1}\end{array}\right.$,故m≥1;
②当p假q真时,$\left\{\begin{array}{l}{m<\frac{1}{4}}\\{m<1}\end{array}\right.$,故m<$\frac{1}{4}$,
综上,实数m的范围是(-∞,$\frac{1}{4}$)∪[1,+∞).
点评 本题考查了二次函数的性质,考查复合命题的判断,是一道中档题.

练习册系列答案
相关题目
2.函数$f(x)=lgx-\frac{11}{x}$的零点所在区间为( )
| A. | (8,9) | B. | (9,10) | C. | (10,11) | D. | (11,12) |
3.某几何体的三视图如图所示,则该几何体的表面积为( )


| A. | 2π+12 | B. | π+12 | C. | 2π+24 | D. | π+24 |
13.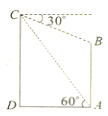 如图,在热气球C正前方有一高为m的建筑物AB,在建筑物底部A测得C的仰角为60°,同时在C处测得建筑物顶部B的仰角为30°,则此时热气球的高度CD为( )
如图,在热气球C正前方有一高为m的建筑物AB,在建筑物底部A测得C的仰角为60°,同时在C处测得建筑物顶部B的仰角为30°,则此时热气球的高度CD为( )
 如图,在热气球C正前方有一高为m的建筑物AB,在建筑物底部A测得C的仰角为60°,同时在C处测得建筑物顶部B的仰角为30°,则此时热气球的高度CD为( )
如图,在热气球C正前方有一高为m的建筑物AB,在建筑物底部A测得C的仰角为60°,同时在C处测得建筑物顶部B的仰角为30°,则此时热气球的高度CD为( )| A. | $\sqrt{2}m$ | B. | $\sqrt{3}m$ | C. | $\frac{{3\sqrt{3}}}{2}m$ | D. | $\frac{3}{2}m$ |
7.点P到直线y=3的距离比到点F(0,-1)的距离大2,则点P的轨迹方程为( )
| A. | y2=4x | B. | y2=-4x | C. | x2=4y | D. | x2=-4y |
8.已知全集U={1,2,3,4,5,6,7,8},A={2,3,5,6},B={1,3,4,6,7},M={x|x∈A,且x∉B},则M=( )
| A. | {2,5} | B. | {3,6} | C. | {2,5,6} | D. | {2,3,5,6,8} |