题目内容
2.函数$f(x)=lgx-\frac{11}{x}$的零点所在区间为( )| A. | (8,9) | B. | (9,10) | C. | (10,11) | D. | (11,12) |
分析 判断函数$f(x)=lgx-\frac{11}{x}$在(0,+∞)上单调递增且连续,从而由零点判定定理判断即可.
解答 解:函数函数$f(x)=lgx-\frac{11}{x}$在(0,+∞)上单调递增且连续,
f(10)=1-$\frac{11}{10}$<0,
f(11)=lg11-1>0;
f(10)f(11)<0,
由函数的零点判定定理可知:函数$f(x)=lgx-\frac{11}{x}$的零点所在的区间为(10,11);
故选:C.
点评 本题考查了函数的零点的判断与应用,属于基础题.

练习册系列答案
相关题目
10.已知$tan(α+β)=\frac{1}{2},tanβ=\frac{1}{3}$,则$tan(α-\frac{π}{4})$=( )
| A. | $\frac{3}{4}$ | B. | $-\frac{3}{4}$ | C. | $\frac{1}{7}$ | D. | $\frac{6}{7}$ |
17.已知集合$A=\{y|y=\sqrt{x}\}$,B={x|y=ln(1-x)},则A∩B=( )
| A. | {x|0≤x<e} | B. | {x|0≤x<1} | C. | {x|1≤x<e} | D. | {x|x≥0} |
11.已知程序框图如图所示,当输入x=2时,输出结果为( )


| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
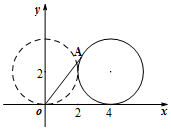 如图,半径为2的圆圆心的初始位置坐标为(0,2),圆上一点A坐标为(0,0).圆沿x轴正向滚动,当圆滚动到圆心位于(4,2)时,A点坐标为(4-2sin2,2-2cos2).
如图,半径为2的圆圆心的初始位置坐标为(0,2),圆上一点A坐标为(0,0).圆沿x轴正向滚动,当圆滚动到圆心位于(4,2)时,A点坐标为(4-2sin2,2-2cos2).