题目内容
点A(1,1)在圆C:x2+y2-x+y+m=0的外部.
(1)求实数m的取值范围;
(2)若m=-
,且过点A(1,1)的直线l被圆C截得的弦长为
,求直线l的方程.
(1)求实数m的取值范围;
(2)若m=-
| 1 |
| 4 |
| 2 |
考点:直线与圆相交的性质,圆与圆的位置关系及其判定
专题:直线与圆
分析:(1)由已知条件得
,由此能求出m的取值范围.
(2)m=-
时,圆C:(x-
)2+(y+
)2=
,由此利用弦长公式能求出直线方程.
|
(2)m=-
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
解答:
解:(1)∵点A(1,1)在圆C:x2+y2-x+y+m=0的外部,
∴
,
解得:-2<m<
,
∴m的取值范围是(-2,
).…(4分)
(2)m=-
时,圆C:x2+y2-x+y-
=0,
即(x-
)2+(y+
)2=
,
当斜率不存在时,直线x=1满足题意.…(6分)
当斜率存在时,设直线方程为y-1=k(x-1),
由题意可知:圆心到直线kx-y-k+1=0的距离为
,…(8分)
∴
=
,解得:k=
,
∴直线方程为4x-3y-1=0,…(11分)
综上:所求直线方程为x=1或4x-3y-1=0.…(12分)
∴
|
解得:-2<m<
| 1 |
| 2 |
∴m的取值范围是(-2,
| 1 |
| 2 |
(2)m=-
| 1 |
| 4 |
| 1 |
| 4 |
即(x-
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
当斜率不存在时,直线x=1满足题意.…(6分)
当斜率存在时,设直线方程为y-1=k(x-1),
由题意可知:圆心到直线kx-y-k+1=0的距离为
| 1 |
| 2 |
∴
| 1 |
| 2 |
|
| ||||
|
| 4 |
| 3 |
∴直线方程为4x-3y-1=0,…(11分)
综上:所求直线方程为x=1或4x-3y-1=0.…(12分)
点评:本题考查实数的取值范围的求法,考查直线方程的求法,是中档题,解题时要注意直线的弦长公式和点到直线的距离公式的合理运用.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
 已知圆C:(x-1)2+(y-1)2=2经过椭圆Γ:
已知圆C:(x-1)2+(y-1)2=2经过椭圆Γ:
 如图,已知⊙O的直径AB=3,点C为⊙O上异于A,B的一点,VC⊥平面ABC,且VC=2,点M为线段VB的中点.
如图,已知⊙O的直径AB=3,点C为⊙O上异于A,B的一点,VC⊥平面ABC,且VC=2,点M为线段VB的中点.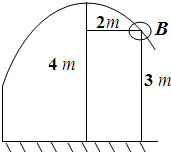 有一次姚明投篮时,测得投篮的轨迹是抛物线,如图所示,抛物线最高点离地面距离4m,篮筐B高为3m,篮筐中心离最高点的水平距离为2m,求投中时抛物线的方程?
有一次姚明投篮时,测得投篮的轨迹是抛物线,如图所示,抛物线最高点离地面距离4m,篮筐B高为3m,篮筐中心离最高点的水平距离为2m,求投中时抛物线的方程?