题目内容
数列{an}的前n项和记为Sn,已知a1=1,Sn=
an+1,(n=1,2,3,…)
(Ⅰ)求数列{Sn}的通项公式;
(Ⅱ)设Tn=S1+S2+S3+…+Sn,求Tn.
| n |
| n+2 |
(Ⅰ)求数列{Sn}的通项公式;
(Ⅱ)设Tn=S1+S2+S3+…+Sn,求Tn.
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(Ⅰ)由已知条件推导出
=
,由此利用累积法能求出数列{Sn}的通项公式.
(Ⅱ)由Sn ═n•2n-1.Tn=S1+S2+S3+…+Sn,利用错位相减法能求出Tn=(n-1)•2n+1.
| Sn+1 |
| Sn |
| 2(n+1) |
| n |
(Ⅱ)由Sn ═n•2n-1.Tn=S1+S2+S3+…+Sn,利用错位相减法能求出Tn=(n-1)•2n+1.
解答:
解:(Ⅰ)∵数列{an}的前n项和记为Sn,a1=1,
Sn=
an+1=
(Sn+1-Sn),
∴
=
,
∴Sn=S1×
×
×…×
=1×
×
×…×
=n•2n-1.
(Ⅱ)∵Tn=S1+S2+S3+…+Sn
∴Tn=1×20+2×2+3×22+…+n×2n-1,①
2Tn=1×2+2×22+3×23+…+n×2n,②
①-②,得-Tn=1+2+22+…+2n-1-n×2n
=
-n•2n
∴Tn=(n-1)•2n+1.
Sn=
| n |
| n+2 |
| n |
| n+2 |
∴
| Sn+1 |
| Sn |
| 2(n+1) |
| n |
∴Sn=S1×
| S2 |
| S1 |
| S3 |
| S2 |
| Sn |
| Sn-1 |
=1×
| 2(1+1) |
| 1 |
| 2(2+1) |
| 2 |
| 2n |
| n-1 |
(Ⅱ)∵Tn=S1+S2+S3+…+Sn
∴Tn=1×20+2×2+3×22+…+n×2n-1,①
2Tn=1×2+2×22+3×23+…+n×2n,②
①-②,得-Tn=1+2+22+…+2n-1-n×2n
=
| 1-2n |
| 1-2 |
∴Tn=(n-1)•2n+1.
点评:本题考查数列的通项公式的求法,考查数列的前n项和的求法,解题时要认真审题,注意错位相减法的合理运用.

练习册系列答案
相关题目
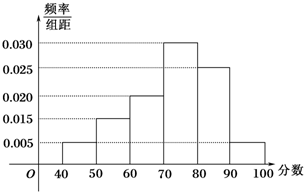 从参加高一年级某次模块考试中抽出80名学生,其数学成绩(均为整数)的频率分布直方图如图所示.
从参加高一年级某次模块考试中抽出80名学生,其数学成绩(均为整数)的频率分布直方图如图所示.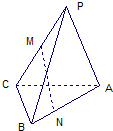 如图P是△ABC所在平面外一点,PA=PB,CB⊥平面PAB,M是PC的中点,N是AB上的点,AN=3NB.求证:MN⊥AB.
如图P是△ABC所在平面外一点,PA=PB,CB⊥平面PAB,M是PC的中点,N是AB上的点,AN=3NB.求证:MN⊥AB. 在如图的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点.
在如图的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点.