题目内容
已知0<a≤
,若f(x)=ax2-2x+1在区间[1,3]上的最大值为M(a),最小值为N(a),令g(a)=M(a)-N(a).
(1)求函数g(a)的表达式;
(2)判断函数g(a)的单调性(只需说明,不用证明),并求g(a)的最小值.
| 1 |
| 3 |
(1)求函数g(a)的表达式;
(2)判断函数g(a)的单调性(只需说明,不用证明),并求g(a)的最小值.
考点:二次函数的性质
专题:函数的性质及应用
分析:(1)首先判断出函数f(x)=ax2-2x+1在区间[1,3]上为单调减函数,然后求出M(a)、N(a),进而求出g(a)的表达式即可;
(2)由一次函数的性质知,g(a)=-8a+4在区间(0,
]单调减,a为
时,g(a)取最小值,代入求解即可.
(2)由一次函数的性质知,g(a)=-8a+4在区间(0,
| 1 |
| 3 |
| 1 |
| 3 |
解答:
解:(1)函数f(x)=ax2-2x+1的对称轴为x=
∵0<a≤
∴
≥3
∴函数f(x)=ax2-2x+1在区间[1,3]上为单调减函数
∴M(a)=f(1)=a-1,N(a)=f(3)=9a-5
∵g(a)=M(a)-N(a)
∴g(a)=-8a+4(0<a≤
)
(2)由一次函数的性质知,g(a)=-8a+4在区间(0,
]单调减,
∴a为
时,g(a)取最小值;
∵g(
)=-8×
+4=
,
函数g(a)min=g(
)=
.
| 1 |
| a |
∵0<a≤
| 1 |
| 3 |
∴
| 1 |
| a |
∴函数f(x)=ax2-2x+1在区间[1,3]上为单调减函数
∴M(a)=f(1)=a-1,N(a)=f(3)=9a-5
∵g(a)=M(a)-N(a)
∴g(a)=-8a+4(0<a≤
| 1 |
| 3 |
(2)由一次函数的性质知,g(a)=-8a+4在区间(0,
| 1 |
| 3 |
∴a为
| 1 |
| 3 |
∵g(
| 1 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
函数g(a)min=g(
| 1 |
| 3 |
| 4 |
| 3 |
点评:本题主要考查了二次函数的性质及其运用,考查了函数的表达式以及最值的求法,属于中档题.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
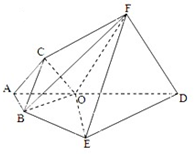 如图,ABEDFC为多面体,平面ABED与平面ACFD垂直,点O在线段AD上,OA=1,OD=2,△OAB,△OAC,△ODF,△ODE都是正三角形.
如图,ABEDFC为多面体,平面ABED与平面ACFD垂直,点O在线段AD上,OA=1,OD=2,△OAB,△OAC,△ODF,△ODE都是正三角形. 在如图的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点.
在如图的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点.