题目内容
19.设函数f(x)=mx2-mx-1,g(x)=$\frac{f(x)}{x-1}$.(1)若对任意x∈[1,3],不等式f(x)<5-m恒成立,求实数m的取值范围;
(2)当m=-$\frac{1}{4}$时,确定函数g(x)在区间(3,+∞)上的单调性.
分析 (1)利用f(x)<5-m,推出m<$\frac{6}{{x}^{2}-x+1}$,设h(x)=$\frac{6}{{x}^{2}-x+1}$,则当x∈[1,3]时,m<h(x)恒成立.利用二次函数的单调性求解m的取值范围.
(2)推出g(x)=-($\frac{x}{4}$+$\frac{1}{x-1}$).设x1>x2>3,则g(x1)-g(x2)=(x1-x2)($\frac{1}{({x}_{1}-1)({x}_{2}-1)}$-$\frac{1}{4}$),利用函数的单调性的定义证明即可.
解答 解:(1)由f(x)<5-m,得mx2-mx-1<5-m,即m(x2-x+1)<6.
因为x2-x+1=(x-$\frac{1}{2}$)2+$\frac{3}{4}$>0,则m<$\frac{6}{{x}^{2}-x+1}$.(3分)
设h(x)=$\frac{6}{{x}^{2}-x+1}$,则当x∈[1,3]时,m<h(x)恒成立.
因为y=x2-x+1在区间[1,3]上是增函数,
则h(x)在区间[1,3]上是减函数,h(x)min=h(3)=$\frac{6}{7}$,
所以m的取值范围是(-∞,$\frac{6}{7}$). (6分)
(2)因为f(x)=mx(x-1)-1,则g(x)=mx-$\frac{1}{x-1}$.
当m=-$\frac{1}{4}$时,g(x)=-($\frac{x}{4}$+$\frac{1}{x-1}$). (7分)
设x1>x2>3,则g(x1)-g(x2)=$\frac{{x}_{2}}{4}+\frac{1}{{x}_{2}-1}$-$\frac{{x}_{1}}{4}$-$\frac{1}{{x}_{1}-1}$=$\frac{{x}_{2}-{x}_{1}}{4}+\frac{{x}_{1}-{x}_{2}}{({x}_{1}-1)({x}_{2}-1)}$
=(x1-x2)($\frac{1}{({x}_{1}-1)({x}_{2}-1)}$-$\frac{1}{4}$)(10分)
因为x1-1>x2-1>2,则(x1-1)(x2-1)>4,
得$\frac{1}{({x}_{1}-1)({x}_{2}-1)}$<$\frac{1}{4}$,
又x1-x2>0,则g(x1)-g(x2)<0,
即g(x1)<g(x2),所以g(x)在区间(3,+∞)上是减函数.(13分)
点评 本题考查函数恒成立,二次函数的简单性质以及函数的单调性的定义的应用,考查转化思想以及计算能力.

 每课必练系列答案
每课必练系列答案| A. | y=3-x | B. | y=-2x | C. | y=log0.1x | D. | y=x${\;}^{\frac{1}{2}}$ |
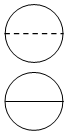 如图,某几何体的正视图和俯视图是两个半径相等的圆,侧视图中两条半径相互垂直.若该几何体的表面积是4πa2,则它的体积是( )
如图,某几何体的正视图和俯视图是两个半径相等的圆,侧视图中两条半径相互垂直.若该几何体的表面积是4πa2,则它的体积是( )| A. | $\frac{4}{3}π{a^3}$ | B. | πa3 | C. | $\frac{2}{3}π{a^3}$ | D. | $\frac{1}{3}π{a^3}$ |
| A. | 12 | B. | 13 | C. | 14 | D. | 15 |
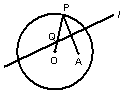 如图,圆O的半径为定长r,A是圆O内的一定点,P为圆上任意 一点,线段AP的垂直平分线l和半径OP相交于点Q,当点P在圆周上运动时,点Q的轨迹是( )
如图,圆O的半径为定长r,A是圆O内的一定点,P为圆上任意 一点,线段AP的垂直平分线l和半径OP相交于点Q,当点P在圆周上运动时,点Q的轨迹是( )