题目内容

7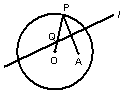．如图，圆O的半径为定长r，A是圆O内的一定点，P为圆上任意 一点，线段AP的垂直平分线l和半径OP相交于点Q，当点P在圆周上运动时，点Q的轨迹是（　　）
A．直线B．圆C．椭圆D．双曲线

分析 由线段AP的垂直平分线l与半径OP相交于点Q，可得QA=QP，进而可得OQ+QA=r，从而曲线是以A、O为焦点，长轴长为r的椭圆．

解答 解：由题意：QA=QP，
∵OP=OQ+QP=r，
∴OQ+QA=r．A是圆O内的一定点，r＞|OA|，
故曲线是以A、O为焦点，长轴长为r的椭圆，
故选：C．

点评 本小题主要考查椭圆的定义、轨迹方程等基础知识，考查运算求解能力，考查化归与转化思想．熟练掌握椭圆的定义及圆与直线的性质是解决问题的关键．属于基础题．

练习册系列答案
相关题目
17．直线$y=-\frac{{\sqrt{3}}}{3}x+1$和x轴，y轴分别交于点A，B，以线段AB为一边在第一象限内作等边△ABC，则点C的坐标为$（{\sqrt{3}，2}）$．
18．将号码分别为1，2，3，4的四个小球放入一个袋中，这些小球仅号码不同，其余完全相同，甲从袋中摸出一个小球，其号码为a，放回后，乙从此袋中再摸出一个小球，其号码为b，则使不等式a-2b+4＜0成立的事件发生的概率为（　　）
A．$\frac{1}{8}$B．$\frac{3}{16}$C．$\frac{1}{4}$D．$\frac{1}{2}$
15．集合A=（2，3]，B=（1，3），C=[m，+∞），全集为R．
（1）求（∁RA）∩B；
（2）若（A∪B）∩C≠∅，求实数m的取值范围．
2．已知函数f（x）=alnx-bx2，a，b∈R．若f（x）在x=1处与直线y=-$\frac{1}{2}$相切．
（1）求a，b的值；
（2）求f（x）在[$\frac{1}{e}$，e]上的最大值．
12．已知x与y之间的一组数据：
x01234
y13579
则y与x的线性回归方程=x+必过点（2，5）．
19．设函数f（x）=mx2-mx-1，g（x）=$\frac{f（x）}{x-1}$．
（1）若对任意x∈[1，3]，不等式f（x）＜5-m恒成立，求实数m的取值范围；
（2）当m=-$\frac{1}{4}$时，确定函数g（x）在区间（3，+∞）上的单调性．
16．设$f（x）=2cos（ωx-\frac{π}{6}）sinωx-\frac{1}{2}cos（2ωx+π）$，其中ω＞0．
（1）求函数y=f（x）的值域；
（2）若y=f（x）在区间$[{-\frac{3π}{4}，\frac{π}{2}}]$上为增函数，求ω的最大值．
17．（文科）已知函数f（x）=2sin（$\frac{1}{2}$x-$\frac{π}{6}$），x∈R
（1）求它的振幅、周期和初相；
（2）求f（$\frac{4π}{3}$）的值；
（3）求函数的最大值，最小值以及取得最大最小值时的x的取值；
（4）求它的增区间．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网