题目内容
4．
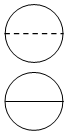如图，某几何体的正视图和俯视图是两个半径相等的圆，侧视图中两条半径相互垂直．若该几何体的表面积是4πa2，则它的体积是（ ）| A． | $\frac{4}{3}π{a^3}$ | B． | πa3 | C． | $\frac{2}{3}π{a^3}$ | D． | $\frac{1}{3}π{a^3}$ |
分析 由已知中正视图和俯视图是两个半径相等的圆，侧视图中两条半径相互垂直．可得该几何体是四分之三球，进而得到答案．
解答 解：由已知中正视图和俯视图是两个半径相等的圆，侧视图中两条半径相互垂直．
可得该几何体是四分之三球，
设球半径为R，则3πR2+2×$\frac{1}{2}$πR2=4πR2=4πa2，
即R=a，
故它的体积是：V=$\frac{3}{4}×\frac{4}{3}{πR}^{3}$=πa3
故选：B
点评 本题考查的知识点是球的体积和表面积，简单几何体的三视图，难度中档．
练习册系列答案
相关题目
14．已知复数z1=$\frac{3+i}{1-i}$的实部为a，复数z2=i（2+i）的虚部为b，复数z=b+ai的共轭复数在复平面内的对应点在（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
12．已知x与y之间的一组数据：
则y与x的线性回归方程=x+必过点（2，5）．
| x | 0 | 1 | 2 | 3 | 4 |
| y | 1 | 3 | 5 | 7 | 9 |
9．已知a=sin21°，b=cos72°，c=tan23°，则a，b，c的大小关系是（ ）
| A． | a＞b＞c | B． | b＞a＞c | C． | c＞b＞a | D． | c＞a＞b |