题目内容

设a＞0且a≠1，命题p：函数f（x）=ax在R上是增函数，命题q：函数g（x）=（a-2）x3在R上是减函数，则p是q的（　　）
A、充分不必要条件
B、必要不充分条件
C、充分必要条件
D、既不充分也不必要条件
考点：必要条件、充分条件与充要条件的判断
专题：函数的性质及应用,简易逻辑
分析：根据指数函数和对数函数的单调性，结合充分条件和必要条件的定义即可得到结论．
解答： 解：若函数f（x）=ax在R上是增函数，则a＞1，当a=2时，g（x）=（a-2）x3=0在R上是减函数，不成立，即充分性不成立．
若函数g（x）=（a-2）x3在R上是减函数，则a-2＜0，此时a＜2，当0＜a＜1时，函数f（x）=ax在R上是减函数，即必要性不成立，
故p是q的既不充分也不必要条件，
故选：D．
点评：本题主要考查充分条件和必要条件的判断，利用函数的单调性是解决本题的关键，比较基础．
练习册系列答案
相关题目
己知 a，b∈R，i是虚数单位，若 
(1+ai)(1-i)
b+i
=2-i，则a+bi=
 
．
已知向量|
a
|=1，|
b
|=2，
a
•
b
=1，则向量
a
与
b
的夹角为
 
．
设有长为a，宽为b的矩形，其底边在半径为R的半圆的直径所在的直线上，另两个顶点正好在半圆的圆周上，则此矩形的周长最大时，
a
b
=
 
．
下列程序语句的算法功能是（　　）
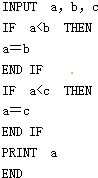
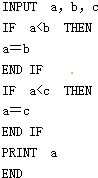
A、输出a，b，c三个数中的最大数
B、输出a，b，c三个数中的最小数
C、将a，b，c按从小到大排列
D、将a，b，c按从大到小排列
复数
2
1+i
（i为虚数单位）的虚部是（　　）
A、1B、-1C、-iD、i
某几何体的三视图及部分数据如图所示，则此几何体的表面积是（　　） 
A、
3
2
B、
3
C、3+4
3
D、3+3
3
已知数列{an}是等差数列，且a3+a9=4，那么数列{an}的前11项和等于（　　）
A、22B、24C、44D、48
设复数z=1+
2
i
（其中i为虚数单位），则z+3
.
z
的虚部为（　　）
A、4iB、4C、-4iD、-4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网