题目内容
某几何体的三视图及部分数据如图所示，则此几何体的表面积是（ ）
A、
| ||
B、
| ||
C、3+4
| ||
D、3+3
|
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：几何体是直三棱柱，根据三视图判断三棱柱的侧棱长、底面三角形的形状及相关几何量的数据，把数据直三棱柱的表面积公式计算．
解答：
解：由三视图知：几何体是直三棱柱，三棱柱的侧棱长为
，
底面是直角边长分别为
、1的直角三角形，斜边长为2，
∴几何体的表面积S=2×
×
×1+（1+2+
）×
=
+3
+3=3+4
．
故选：C．
| 3 |
底面是直角边长分别为
| 3 |
∴几何体的表面积S=2×
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
故选：C．
点评：本题考查了由三视图求几何体的表面积，根据三视图判断几何体的形状及数据所对应的几何量是关键．
练习册系列答案
相关题目
设a＞0且a≠1，命题p：函数f（x）=ax在R上是增函数，命题q：函数g（x）=（a-2）x3在R上是减函数，则p是q的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
复数
的虚部是（ ）
| 5i |
| 1+2i |
| A、1 | B、-1 | C、i | D、-i |
对于函数f（x）与g（x），若存在区间[m，n]（m＜n），使得f（x）与g（x）在区间[m，n]上的值域相等，则称f（x）与g（x）为等值函数，若f（x）=ax（a＞1）与g（x）=logax为等值函数，则a的取值范围为（ ）
A、（1，
| ||
B、（
| ||
C、（1，e
| ||
D、（e
|
设变量z，y满足约束条件
，则目标函数z=
的最大值为（ ）
|
| y |
| x |
A、
| ||
| B、3 | ||
| C、6 | ||
| D、9 |
设全集U={3，4，5，6}，集合A={3，5}，则∁UA=（ ）
| A、{4，5} | B、{6} |
| C、{4，6} | D、{3} |
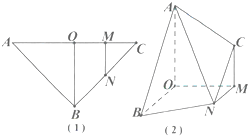如图（1），在三角形ABC中，BA=BC=2