题目内容
9.已知抛物线C:y2=4x,直线l:x=-1.(1)若曲线C上存在一点Q,它到l的距离与到坐标原点的距离相等,求Q的坐标;
(2)过直线l上任一点P作抛物线的两条切线,切点记为A,B,求证:直线AB过定点.
分析 (1)设Q(x,y),则(x+1)2=x2+y2,即y2=2x+1,与抛物线方程联立,得Q的坐标;
(2)先通过特例求出定点,再证明一般性结论.
解答 (1)解:设Q(x,y),则(x+1)2=x2+y2,即y2=2x+1,
与抛物线方程联立,得Q($\frac{1}{2}$,$±\sqrt{2}$);
(2)证明:设直线方程为y-t=k(x+1)(k≠0),代入抛物线方程整理得ky2-4y+4t+4k=0,
△=0,可得k2+kt-1=0.
特别地,t=0,k=±1,这时切点为A(1,2),B(1,-2),AB过定点F(1,0).
一般地,k1+k2=t,k1k2=-1,切点为A($\frac{1}{{{k}_{1}}^{2}}$,$\frac{2}{{k}_{1}}$),B($\frac{1}{{{k}_{2}}^{2}}$,$\frac{2}{{k}_{2}}$),
∴$\overrightarrow{FA}$=($\frac{1}{{{k}_{1}}^{2}}$-1,$\frac{2}{{k}_{1}}$),$\overrightarrow{FB}$=($\frac{1}{{{k}_{2}}^{2}}$-1,$\frac{2}{{k}_{2}}$),
∴($\frac{1}{{{k}_{1}}^{2}}$-1)$\frac{2}{{k}_{2}}$-=$\frac{1}{{{k}_{2}}^{2}}$-1)$\frac{2}{{k}_{1}}$)=0,
∴$\overrightarrow{FA}$∥$\overrightarrow{FB}$,
∴AB过点F(1,0),
综上所述,直线AB过点F(1,0).
点评 本题考查轨迹方程,考查直线过定点,考查学生分析解决问题的能力,属于中档题.

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案| A. | (-5,0) | B. | (-3,0) | C. | (0,4) | D. | (-5,4) |
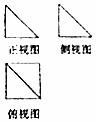 如图是一个几何体的三视图,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,则该多面体的各条棱中最长棱的长度为( )
如图是一个几何体的三视图,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,则该多面体的各条棱中最长棱的长度为( )| A. | $\sqrt{7}$ | B. | $\sqrt{5}$ | C. | 2 | D. | $\sqrt{3}$ |
| A. | (-∞,1] | B. | (-∞,-1] | C. | [-1,+∞) | D. | [1,+∞) |
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |