题目内容
17．已知函数$f（x）=\left\{\begin{array}{l}{e^x}+a，x≤0\\{x^2}+1+a．x＞0\end{array}\right.$，a为实数，若f（2-x）≥f（x），则x的取值范围是（ ）| A． | （-∞，1] | B． | （-∞，-1] | C． | [-1，+∞） | D． | [1，+∞） |
分析 根据分段函数的单调性即可判断．
解答 解：由题意可得函数f（x）在R上为单调递增函数，
∵f（2-x）≥f（x），
∴2-x≥x，
解得x≤1，
故选：A
点评 本题考查函数的单调性的运用：解不等式，属于基础题．
练习册系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
7．设集合A={x∈R|x-1＞0}，B={x∈R|x＜0}，C={x∈R|x（x-1）＞0}，则“x∈A∪B“是“x∈C“的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充分必要条件 | D． | 既不充分也不必要条件 |
8．设函数f（x）=$\left\{\begin{array}{l}{{e}^{x}，x≥0}\\{{x}^{2}，x＜0}\end{array}\right.$，若方程f（f（x））=a（a＞0）恰有两个不相等的实根x1，x2，则e${\;}^{{x}_{1}}$•e${\;}^{{x}_{2}}$的最大值为（ ）
| A． | $\frac{1}{{e}^{2}}$ | B． | 2（ln2-1） | C． | $\frac{4}{{e}^{2}}$ | D． | ln2-1 |
12．已知函数f（x）=$\left\{\begin{array}{l}{{2}^{x-m}，x＜2}\\{\frac{mx}{4{x}^{2}+16}，x≥2}\end{array}\right.$，对任意的x1∈[2，+∞）总存在x2∈（-∞，2]，使得f（x1）=f（x2），则实数m的取值范围是（ ）
| A． | [2，4） | B． | （-∞，4] | C． | [3，4） | D． | （0，4） |
2．
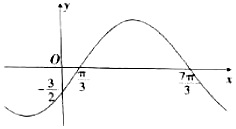已知函数$f（x）=Asin（{ωx+φ}）（{A＞0，ω＞0，|φ|＜\frac{π}{2}}）$的部分图象如图所示，将函数y=f（x）的图象向左平移$\frac{4π}{3}$个单位，得到函数y=g（x）的图象，则函数y=g（x）在区间$[{\frac{π}{2}，\frac{5π}{2}}]$上的最大值为（ ）
已知函数$f（x）=Asin（{ωx+φ}）（{A＞0，ω＞0，|φ|＜\frac{π}{2}}）$的部分图象如图所示，将函数y=f（x）的图象向左平移$\frac{4π}{3}$个单位，得到函数y=g（x）的图象，则函数y=g（x）在区间$[{\frac{π}{2}，\frac{5π}{2}}]$上的最大值为（ ）| A． | 3 | B． | $\frac{{3\sqrt{3}}}{2}$ | C． | $\frac{{3\sqrt{2}}}{2}$ | D． | $\frac{{\sqrt{2}}}{2}$ |