题目内容
20.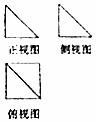 如图是一个几何体的三视图,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,则该多面体的各条棱中最长棱的长度为( )
如图是一个几何体的三视图,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,则该多面体的各条棱中最长棱的长度为( )| A. | $\sqrt{7}$ | B. | $\sqrt{5}$ | C. | 2 | D. | $\sqrt{3}$ |
分析 几何体为四棱锥,底面是正方形,根据三视图数据计算出最长棱即可.
解答 解:由三视图可知几何体为四棱锥P-ABCD,其中底面ABCD为正方形,PA⊥平面ABCD,
且PA=AB=1,
∴几何体的最长棱为PC=$\sqrt{{1}^{2}+{\sqrt{2}}^{2}}$=$\sqrt{3}$.
故选:D
点评 本题考查的知识点是球的体积与表面积,简单几何体的三视图,难度中档.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.设函数f(x)=$\left\{\begin{array}{l}{{e}^{x},x≥0}\\{{x}^{2},x<0}\end{array}\right.$,若方程f(f(x))=a(a>0)恰有两个不相等的实根x1,x2,则e${\;}^{{x}_{1}}$•e${\;}^{{x}_{2}}$的最大值为( )
| A. | $\frac{1}{{e}^{2}}$ | B. | 2(ln2-1) | C. | $\frac{4}{{e}^{2}}$ | D. | ln2-1 |
15.用三段论演绎推理:任何实数的平方都大于0,a∈R,则a2>0.对于这段推理,下列说法正确的是( )
| A. | 大前提错误,导致结论错误 | B. | 小前提错误,导致结论错误 | ||
| C. | 推理形式错误,导致结论错误 | D. | 推理没有问题,结论正确 |
12.已知函数f(x)=$\left\{\begin{array}{l}{{2}^{x-m},x<2}\\{\frac{mx}{4{x}^{2}+16},x≥2}\end{array}\right.$,对任意的x1∈[2,+∞)总存在x2∈(-∞,2],使得f(x1)=f(x2),则实数m的取值范围是( )
| A. | [2,4) | B. | (-∞,4] | C. | [3,4) | D. | (0,4) |
10.函数$f(x)=\frac{3}{x-4}+\sqrt{{2^x}-4}$的定义域是( )
| A. | [2,4) | B. | [2,4)∪(4,+∞) | C. | (2,4)∪(4,+∞) | D. | [2,+∞) |
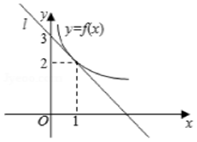 如图所示,y=f(x)是可导函数,直线l:y=kx+3是曲线y=f(x)在x=1处的切线,若h(x)=xf(x),则h(x)在x=1处的切线方程为x-y+1=0.
如图所示,y=f(x)是可导函数,直线l:y=kx+3是曲线y=f(x)在x=1处的切线,若h(x)=xf(x),则h(x)在x=1处的切线方程为x-y+1=0.