题目内容
求证：
-2
＞
-
（用分析法）
| 6 |
| 2 |
| 5 |
| 7 |
考点：综合法与分析法(选修）
专题：不等式
分析：本题指定用分析法证明，通过分析得到易证命题，从而证得原命题成立．
解答：
证明：要证：
-2
＞
-
，
只要证：
+
＞2
+
，
只要证：(
+
)2＞(2
+
)2，
只要证：13+2
＞13+2
，
只要证：
＞
，
只要证：42＞40．
∵42＞40，
∴原命题成立．
| 6 |
| 2 |
| 5 |
| 7 |
只要证：
| 7 |
| 6 |
| 2 |
| 5 |
只要证：(
| 7 |
| 6 |
| 2 |
| 5 |
只要证：13+2
| 42 |
| 40 |
只要证：
| 42 |
| 40 |
只要证：42＞40．
∵42＞40，
∴原命题成立．
点评：本题考查的是用分析法证明不等式，本题难度不大，属于基础题．
练习册系列答案
相关题目
圆心为（1，-1），半径为5的圆的标准方程为（ ）
| A、（x-1）2+（y+1）2=5 |
| B、（x+1）2+（y-1）2=5 |
| C、（x-1）2+（y+1）2=25 |
| D、（x+1）2+（y-1）2=25 |
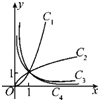图中的曲线是幂函数y=xn在第一象限的图象，已知n可取±2，±| 1 |
| 2 |
A、-2，-
| ||||
B、2，
| ||||
C、-
| ||||
D、2，
|
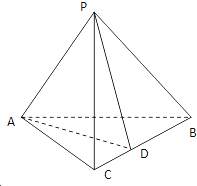如图，在三棱锥P-ABC中，AC=BC=2，∠ACB=90°，AP=BP=AB，PC⊥AC，点D为BC中点．
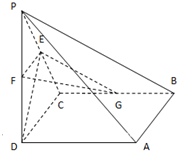如图所示，在四棱锥P-ABCD中，底面ABCD为正方形，PD⊥平面ABCD，PD=AB=2，E、F分别为PC、PD的中点．