题目内容
16.某机械研究所对新研发的某批次机械元件进行寿命追踪调查,随机抽查的200个机械元件情况如下:| 使用时间(单位:天) | 10:20 | 21:30 | 31:40 | 41:50 | 51:60 |
| 个数 | 10 | 40 | 80 | 50 | 20 |
| A. | $\frac{13}{16}$ | B. | $\frac{27}{64}$ | C. | $\frac{25}{32}$ | D. | $\frac{27}{32}$ |
分析 基本事件总数n=${C}_{200}^{3}$,由题意得:使用寿命在30天以上共150个,由此求出至少有2个元件的使用寿命在30天以上包含的基本事件个数m=${C}_{50}^{1}{C}_{150}^{2}+{C}_{150}^{3}$,从而能求出至少有2个元件的使用寿命在30天以上的概率.
解答 解:随机抽查的200个机械元件,从该批次机械元件随机抽取3个,
基本事件总数n=${C}_{200}^{3}$,
由题意得:使用寿命在30天以上共150个,
至少有2个元件的使用寿命在30天以上包含的基本事件个数m=${C}_{50}^{1}{C}_{150}^{2}+{C}_{150}^{3}$,
故至少有2个元件的使用寿命在30天以上的概率是:
P=$\frac{{{C}_{50}^{1}C}_{150}^{2}{+C}_{150}^{3}}{{C}_{200}^{3}}$=$\frac{27}{32}$.
故选:D.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
 中国传统文化中很多内容体现了数学的对称美,如图所示的太极图是由黑白两个鱼形纹组成的圆形图案,充分展现了相互转化、对称统一的形式美、和谐美,给出定义:能够将圆O的周长和面积同时平分的函数称为这个圆的“优美函数”,给出下列命题:
中国传统文化中很多内容体现了数学的对称美,如图所示的太极图是由黑白两个鱼形纹组成的圆形图案,充分展现了相互转化、对称统一的形式美、和谐美,给出定义:能够将圆O的周长和面积同时平分的函数称为这个圆的“优美函数”,给出下列命题: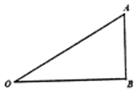 如图,某儿童公园设计一个直角三角形游乐滑梯,AO为滑道,∠OBA为直角,OB=20米,设∠AOB=θrad,一个小朋友从点A沿滑道往下滑,记小朋友下滑的时间为t秒,已知小朋友下滑的长度s与t2和sinθ的积成正比,当$θ=\frac{π}{6}$时,小朋友下滑2秒时的长度恰好为10米.
如图,某儿童公园设计一个直角三角形游乐滑梯,AO为滑道,∠OBA为直角,OB=20米,设∠AOB=θrad,一个小朋友从点A沿滑道往下滑,记小朋友下滑的时间为t秒,已知小朋友下滑的长度s与t2和sinθ的积成正比,当$θ=\frac{π}{6}$时,小朋友下滑2秒时的长度恰好为10米.