题目内容
8.设a为实数,函数f(x)=ex-x+a,x∈R.(1)求f(x)在区间[-1,2]上的最值;
(2)求证:当a>-1,且x>0时,${e^x}>\frac{1}{2}{x^2}-ax+1$.
分析 (1)求出函数的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的最值即可;
(2))令$g(x)={e^x}-\frac{1}{2}{x^2}+ax-1,g'(x)={e^x}-x+a$,根据函数的单调性求出g(x)>g(0),证出结论即可.
解答 解:(1)f'(x)=ex-1,令f'(x)=0,则x=0,
x∈(-1,0),f'(x)<0,f(x)为减函数,
x∈(0.2),f'(x)>0,f(x)为增函数,
所以,f(x)min=f(0)=1+a;
又因为$f(-1)={e^{-1}}+1+a,f(2)={e^2}-2+a,f(-1)-f(2)=\frac{1}{e}-3-{e^2}<0$,
所以$f{(x)_{max}}=f(2)={e^2}-2+a$.
(2)证明:令$g(x)={e^x}-\frac{1}{2}{x^2}+ax-1,g'(x)={e^x}-x+a$,
由(1)知,g'(x)≥g'(0)=1+a>0,
所以g(x)在(0,+∞)单调递增,
所以g(x)>g(0)=0,
所以,当a>-1,且x>0时,${e^x}>\frac{1}{2}{x^2}-ax+1$.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及不等式的证明,是一道中档题.

练习册系列答案
相关题目
5.设全集U=R,A={x|x2-x-6<0},B={x|y=lg(x+1)},则图中阴影部分表示的集合为( )
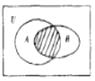

| A. | {x|-3<x<-1} | B. | {x|-3<x<0} | C. | {x|-1<x<3} | D. | {x|x>-1} |
16.某机械研究所对新研发的某批次机械元件进行寿命追踪调查,随机抽查的200个机械元件情况如下:
若以频率为概率,现从该批次机械元件随机抽取3个,则至少有2个元件的使用寿命在30天以上的概率为( )
| 使用时间(单位:天) | 10:20 | 21:30 | 31:40 | 41:50 | 51:60 |
| 个数 | 10 | 40 | 80 | 50 | 20 |
| A. | $\frac{13}{16}$ | B. | $\frac{27}{64}$ | C. | $\frac{25}{32}$ | D. | $\frac{27}{32}$ |

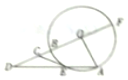 如图,圆O的半径OA与OB相互垂直,E为圆O上一点,直线OB与圆O交于另一点F,与直线AE交于点D,过点E的切线CE交线段于点C,求证:CD2=CB•CF.
如图,圆O的半径OA与OB相互垂直,E为圆O上一点,直线OB与圆O交于另一点F,与直线AE交于点D,过点E的切线CE交线段于点C,求证:CD2=CB•CF.