题目内容
6．${（x-\frac{1}{4x}）^6}$的展开式中常数项为$-\frac{5}{16}$．分析 写出二项展开式的通项，令x的指数为0求得r值，则答案可求．
解答 解：由${T}_{r+1}={C}_{6}^{r}{x}^{6-r}（-\frac{1}{4x}）^{r}=（-\frac{1}{4}）^{r}{C}_{6}^{r}{x}^{6-2r}$，
取6-2r=0，得r=3．
∴${（x-\frac{1}{4x}）^6}$的展开式中常数项为$（-\frac{1}{4}）^{3}{C}_{6}^{3}=-\frac{5}{16}$．
故答案为：-$\frac{5}{16}$．
点评 本题考查二项式系数的性质，关键是熟记展开式的通项，是基础题．
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
17．（x-1）5+5（x-1）4+10（x-1）3+10（x-1）2+5（x-1）+1=（ ）
| A． | x5 | B． | （x-1）5-1 | C． | x5+1 | D． | 1 |
14．命题“?x0∈R，f（x0）≥2或f（x0）≤1”的否定形式是（ ）
| A． | ?x∈R，1＜f（x）＜2 | B． | ?x0∈R，1＜f（x0）＜2 | ||
| C． | ?x∈R，f（x）≥2或f（x）≤1 | D． | ?x0∈R，f（x0）≥2或f（x0）＞1 |
1．若直线x+my-1=0与不等式组$\left\{\begin{array}{l}{x+2y-4≤0}\\{x-y+2≤0}\\{x≥-1}\end{array}\right.$，表示的平面区域有公共点，则实数m的取值范围是（ ）
| A． | [$\frac{1}{2}$，2] | B． | [$\frac{1}{3}$，3] | C． | （-∞，$\frac{1}{3}$]∪[3，+∞） | D． | （-∞，$\frac{1}{2}$]∪[2，+∞） |
11．已知向量$\overrightarrow{a}$=（3，2），$\overrightarrow{b}$=（-1，1），则|2$\overrightarrow{a}+\overrightarrow{b}$|=（ ）
| A． | $\sqrt{2}$ | B． | $\sqrt{13}$ | C． | 5$\sqrt{2}$ | D． | $\sqrt{2}+2\sqrt{13}$ |
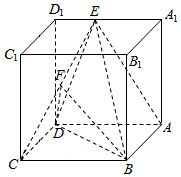如图，正方体ABCD-A1B1C1D1中，点E是A1D1的中点，点F是CE的中点．