题目内容
16.函数y=logsin3(x2-2x)的单调递减区间(2,+∞).分析 正弦函数可知,先求对数函数的定义域,再根据sinπ<sin3<sin$\frac{π}{2}$,0<sin<1,由对数函数的图象可知,$lo{g}_{sin3}({x}^{2}-2x)$的图象是单调递减.
解答 解:有对数函数的定义域可知:x2-2x>0
解得x<0或x>2
由二次函数图象可知当x<0单调递减,当x>2是单调递增的
sinπ<sin3<sin$\frac{π}{2}$,0<sin<1,由对数函数的图象可知,
$lo{g}_{sin3}({x}^{2}-2x)$的图象是单调递减,
根据复合函数的单调性可知,当x>2时函数单调递减,
原函数的单调递减区间为(2,+∞)
故答案为:(2,+∞)
点评 本题考查了对数函数的定义域,单调区间以及复合函数的单调性的问题,都是最常见的知识点,属于基础题.

练习册系列答案
相关题目
7.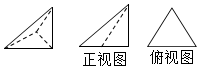 已知三棱锥的直观图及正视图与俯视图如图,其中正视图是直角边为3的等腰直角三角形,俯视图是边长为3的正三角形,则该三棱锥侧视图的面积为( )
已知三棱锥的直观图及正视图与俯视图如图,其中正视图是直角边为3的等腰直角三角形,俯视图是边长为3的正三角形,则该三棱锥侧视图的面积为( )
 已知三棱锥的直观图及正视图与俯视图如图,其中正视图是直角边为3的等腰直角三角形,俯视图是边长为3的正三角形,则该三棱锥侧视图的面积为( )
已知三棱锥的直观图及正视图与俯视图如图,其中正视图是直角边为3的等腰直角三角形,俯视图是边长为3的正三角形,则该三棱锥侧视图的面积为( )| A. | $\frac{9}{2}$ | B. | $\frac{9}{4}$ | C. | $\frac{9\sqrt{3}}{2}$ | D. | $\frac{9\sqrt{3}}{4}$ |
4.已知数列{an}为等差数列,a2+a3=1,a10+a11=9,则a5+a6=( )
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |