题目内容
已知函数f(x)=2cos(ωx+φ)+1(ω>0,0≤φ≤
)的图象与y轴相交于点(0,
+1),且函数的最小正周期为π.
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)当x∈[-
,
]时,求函数f(x)的单调递减区间;
(Ⅲ)若关于x的方程f(x)-k=0(k∈R)在区间[-
,
]上恰有两个不相等的实数根,求实数k的取值范围.
| π |
| 2 |
| 3 |
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)当x∈[-
| π |
| 2 |
| π |
| 2 |
(Ⅲ)若关于x的方程f(x)-k=0(k∈R)在区间[-
| π |
| 2 |
| π |
| 2 |
考点:由y=Asin(ωx+φ)的部分图象确定其解析式,正弦函数的图象
专题:三角函数的图像与性质
分析:(Ⅰ)由周期求出ω,由特殊点的坐标求出φ,可得函数的解析式.
(Ⅱ)令2kπ≤2x+
≤2kπ+π,k∈z,求得x的范围,再结合x∈[-
,
]时,可得函数f(x)的单调递减区间
(Ⅲ)由题意可得函数f(x)的图象和直线y=k在区间[-
,
]上恰有两个不同的交点,数形结合求得故k的范围.
(Ⅱ)令2kπ≤2x+
| π |
| 6 |
| π |
| 2 |
| π |
| 2 |
(Ⅲ)由题意可得函数f(x)的图象和直线y=k在区间[-
| π |
| 2 |
| π |
| 2 |
解答:
 解:(Ⅰ)由函数的最小正周期为
解:(Ⅰ)由函数的最小正周期为
=π,可得ω=2.
把点(0,
+1)代入函数
f(x)=2cos(ωx+φ)+1,可得cosφ=
,
再结合0≤φ≤
,可得φ=
,
∴f(x)=2cos(2x+
)+1.
(Ⅱ)令2kπ≤2x+
≤2kπ+π,k∈z,
求得kπ-
≤x≤kπ+
,
故函数f(x)的减区间为[kπ-
,kπ+
],k∈z.
再结合x∈[-
,
]时,可得函数f(x)的单调递减区间为[-
,
].
(Ⅲ)若关于x的方程f(x)-k=0(k∈R)在区间[-
,
]上恰有两个不相等的实数根,
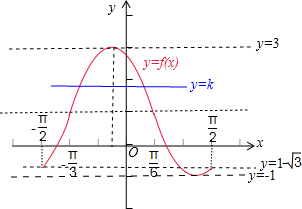
则函数f(x)的图象和直线y=k在区间[-
,
]上恰有两个不同的交点,如图所示:
故k的范围为{k|-1<k<3,且k≠1-
}.
 解:(Ⅰ)由函数的最小正周期为
解:(Ⅰ)由函数的最小正周期为| 2π |
| ω |
把点(0,
| 3 |
f(x)=2cos(ωx+φ)+1,可得cosφ=
| ||
| 2 |
再结合0≤φ≤
| π |
| 2 |
| π |
| 6 |
∴f(x)=2cos(2x+
| π |
| 6 |
(Ⅱ)令2kπ≤2x+
| π |
| 6 |
求得kπ-
| π |
| 12 |
| 5π |
| 12 |
故函数f(x)的减区间为[kπ-
| π |
| 12 |
| 5π |
| 12 |
再结合x∈[-
| π |
| 2 |
| π |
| 2 |
| π |
| 12 |
| 5π |
| 12 |
(Ⅲ)若关于x的方程f(x)-k=0(k∈R)在区间[-
| π |
| 2 |
| π |
| 2 |
则函数f(x)的图象和直线y=k在区间[-
| π |
| 2 |
| π |
| 2 |
故k的范围为{k|-1<k<3,且k≠1-
| 3 |
点评:本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,余弦函数的图象,方程根的存在性以及个数判断,体现了转化、数形结合的数学思想,属于中档题.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
复数z1=1+i,z2=3+ai,且3z1=z2,则a=( )
| A、0 | B、1 | C、2 | D、3 |
 如图,已知圆G:x2-x+y2=0,经过抛物线y2=2px的焦点,过点(m,0)(m<0)倾斜角为
如图,已知圆G:x2-x+y2=0,经过抛物线y2=2px的焦点,过点(m,0)(m<0)倾斜角为 如图所示,在直三棱柱ABC-A1B1C1中,AC=4,BC=2,AB=2AA1=2
如图所示,在直三棱柱ABC-A1B1C1中,AC=4,BC=2,AB=2AA1=2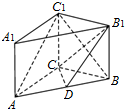 如图,已知在三棱柱ABC-A1B1C1中,AC=4,BC=3,BC1=5,点D在线段AB上,AD=3,BD=2,四边形ACC1A1为正方形.
如图,已知在三棱柱ABC-A1B1C1中,AC=4,BC=3,BC1=5,点D在线段AB上,AD=3,BD=2,四边形ACC1A1为正方形.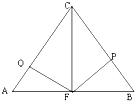 如图,CF是△ABC边AB上的高,FP⊥BC,FQ⊥AC.
如图,CF是△ABC边AB上的高,FP⊥BC,FQ⊥AC.