题目内容
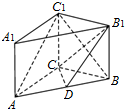 如图,已知在三棱柱ABC-A1B1C1中,AC=4,BC=3,BC1=5,点D在线段AB上,AD=3,BD=2,四边形ACC1A1为正方形.
如图,已知在三棱柱ABC-A1B1C1中,AC=4,BC=3,BC1=5,点D在线段AB上,AD=3,BD=2,四边形ACC1A1为正方形.(1)求证:BC⊥AC1;
(2)请判断AC1是否平行于平面B1CD(不用证明);
(3)求三棱锥C1-CDB1的体积.
考点:棱柱、棱锥、棱台的体积,空间中直线与直线之间的位置关系,直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)运用勾股定理得出BC⊥AC,BC⊥CC1而CC1∩AC=C,再用判断定理得出BC⊥平面AA1C1C,BC⊥AC1
(2)根据直线平面平行的判断定理推导得出:AC1与平面B1CD不平行,
(3)根据体积公式得出VC1-B1DC=VD-B1C1C=
VA-B1C1C.
(2)根据直线平面平行的判断定理推导得出:AC1与平面B1CD不平行,
(3)根据体积公式得出VC1-B1DC=VD-B1C1C=
| 2 |
| 5 |
解答:
解:(1)∵在△ABC中,AC=4,BC=3,AB=5,
∴∠ACB=90°,即BC⊥AC,
△BCC1中,BC=3,CC1=4,BC1=5,
∴BC⊥CC1而CC1∩AC=C,.
∴BC⊥平面AA1C1C,BC⊥AC1.
(2)AC1与平面B1CD不平行.
(3)由已知易知AC⊥平面BCC1,AB:DB=5:2,
∴VC1-B1DC=VD-B1C1C=
VA-B1C1C=
×
×
×3×4×4=
,
∴∠ACB=90°,即BC⊥AC,
△BCC1中,BC=3,CC1=4,BC1=5,
∴BC⊥CC1而CC1∩AC=C,.
∴BC⊥平面AA1C1C,BC⊥AC1.
(2)AC1与平面B1CD不平行.
(3)由已知易知AC⊥平面BCC1,AB:DB=5:2,
∴VC1-B1DC=VD-B1C1C=
| 2 |
| 5 |
| 2 |
| 5 |
| 1 |
| 3 |
| 1 |
| 2 |
| 16 |
| 5 |
点评:本题考查了空间直线平面的平行,垂直,体积,面积问题,属于中档题,难度不大.

练习册系列答案
相关题目
下列结论正确的是( )
A、若向量
| ||||||||||||
B、已知向量
| ||||||||||||
C、“若 θ=
| ||||||||||||
| D、若命题 p:?x∈R,x2-x+1<0,则?p:?x∈R,x2-x+1>0 |
在区间[-1,1]上任取两个数a、b,则点(-1,1)与点(1,1)在直线ax+by+1=0的两侧的概率等于( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知双曲线C:
-
=1(a>0,b>0)的一条渐近线方程是y=-
x,它的一个焦点在抛物线y2=-24x的准线上,则双曲线的方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 已知椭圆
已知椭圆