题目内容

化简：
tan(π-α)sin2(α+
π
2
)cos(2π-α)
cos3(-α-π)tan(α-2π)
．
考点：运用诱导公式化简求值,同角三角函数基本关系的运用
专题：三角函数的求值
分析：直接利用诱导公式化简求值即可．
解答： 解：
tan(π-α)sin2(α+
π
2
)cos(2π-α)
cos3(-α-π)tan(α-2π)

=
-tanαcos2αcosα
-cos3αtanα

=1．
故答案为：1．
点评：本题考查诱导公式的应用，三角函数的化简求值．
练习册系列答案
相关题目
已知cos（
π
2
-φ）=
3
2
，且|φ|＜
π
2
，则tanφ=
 
．
若f（x）=x+
1
x-2
（x＞2）在x=n处取到最小值，则n的值为（　　）
A、
5
2
B、3
C、
7
2
D、4
已知集合A={x||-3＜x+2＜3}，B={x|m＜x＜1}，其中m＜1．
（1）若A∩B={x|-1＜x＜m}，求实数m，n的值；
（2）若A∪（∁UB）=R，求m的取值范围．
计算：
3
sin(-
20
3
π
)
tan
11
3
π-cos
13
4
π•tan（-
35
4
π）．
复数
2a+i
-1+2i
（i是虚数单位）为纯虚数，则实数a的值为（　　）
A、
1
4
B、-
1
4
C、1
D、-1
已知AB是⊙O的弦，P是AB上一点，AB=6
2
，PA=4
2
，OP=3，则⊙O的半径R=
 
．
盒中共有9个球，其中有4个红球，3个黄球和2个绿球，这些球除颜色外完全相同．
（1）规定：进行一次操作指：“从盒中随机取出一个球，若取出的是黄球，则把它放回盒中；
若取出的是红球或绿球，则该球不放回，并另外补一个黄球放入盒中”，求：
①在第一次操作取出的是红球或绿球的条件下，第二次操作取出黄球的概率；
②经过第二次操作后，盒中黄球的个数是4个概率；
（2）从盒中一次随机抽出4个球，其中红球、黄球、绿球的个数分别为x1、x2、x3，随机变量X表示x1、x2、x3的最大数，求X的概率分布列和数学期望E（X）．
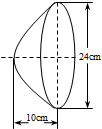如图所示，汽车前灯反光镜与轴截面的交线是抛物线的一部分，灯口所在的圆面与反光镜的轴垂直，灯泡位于抛物线的焦点处．已知灯口的直径是24cm，灯深10cm，那么灯泡与反光镜的顶点（即截得抛物线的顶点）距离为（　　）
A、10cmB、7.2cm
C、3.6cmD、2.4cm

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网