题目内容

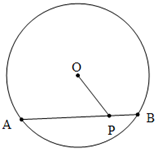
已知AB是⊙O的弦，P是AB上一点，AB=6
2
，PA=4
2
，OP=3，则⊙O的半径R=
 
．
考点：与圆有关的比例线段
专题：立体几何
分析：过点O作OC⊥AB，交AB于点C，连结OA，由垂径定理和勾股定理求出OC⊥AB，PC=PA-AC=
2
，OC=
7
，由此能求出⊙O的半径R．
解答： 解：过点O作OC⊥AB，交AB于点C，连结OA，
∵AB是⊙O的弦，P是AB上一点，AB=6
2
，PA=4
2
，OP=3，
∴OC⊥AB，PC=PA-AC=4
2
-
6
2
2
=
2
，
∴OC=
OP2-PC2
=
9-2
=
7
，
∴R=OA=
OC2+AC2
=
7+18
=5．
故答案为：5．
点评：本题考查圆的半径的求法，是基础题，解题时要认真审题，注意垂径定理和勾股定理的合理运用．
练习册系列答案
相关题目
已知集合M={x|x＞-1}，那么下列结论正确的是（　　）
A、0⊆MB、{0}∈M
C、ϕ∈MD、{0}⊆M
设全集U={1，2，3，4，5，6}，集合A={1，2，3，5}，B={2，4，6}，则（∁UA）∩B为（　　）
A、{2}
B、{4，6}
C、{1，3，5}
D、{2，4，6}
化简：
tan(π-α)sin2(α+
π
2
)cos(2π-α)
cos3(-α-π)tan(α-2π)
．
“a=-3”是“圆x2+y2=1与圆（x+a）2+y2=4相切”的（　　）
A、充分而不必要条件
B、必要而不充分条件
C、充分必要条件
D、既不充分也不必要条件
已知双曲线过点（
3
，2），且它的渐近线方程是y=±2x，则此双曲线的方程是
 
．
设椭圆
x2
4
+
y2
a2
=1和双曲线
x2
a2
-
y2
b2
=1有共同的焦点，连接椭圆的焦点和短轴的一个端点所得直线和双曲线的一条渐近线平行，设双曲线的离心率为e，则e2等于（　　）
A、
5
+1
2
B、
3
+1
2
C、
3
D、
5
已知数列{an}的首项为a1=5，前n项和为Sn，且Sn+1=2Sn+n+5（n∈N+）．
（1）证明：数列{an+1}是等比数列，并求数列{an}的通项公式；
（2）设关于x的函数f（x）=（a1+1）x+（a2+1）x2+…+（an+1）xn，求函数f（x）在点x=1处的导致f′（1）的值．
定义：若m-
1
2
＜x≤m+
1
2
（其中m是整数），则m叫做距实数x最近的整数，记作（x），即（x）=m，对于函数f（x）=|x-（x）|的五个命题，其中正确的有
 
（写出所有正确命题的序号）．
①函数y=f（x）的值域是[0，+∞）；
②函数y=f（x）是偶函数；
③函数y=f（x）是周期函数且最小正周期是1；
④函数y=f（x）的递增区间是[k，k+
1
2
]，k∈z；
⑤函数y=f（x）-lgx有4个零点．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网