题目内容

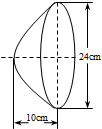如图所示，汽车前灯反光镜与轴截面的交线是抛物线的一部分，灯口所在的圆面与反光镜的轴垂直，灯泡位于抛物线的焦点处．已知灯口的直径是24cm，灯深10cm，那么灯泡与反光镜的顶点（即截得抛物线的顶点）距离为（　　）
A、10cmB、7.2cm
C、3.6cmD、2.4cm
考点：抛物线的应用
专题：计算题,圆锥曲线的定义、性质与方程
分析：先设出抛物线的标准方程y2=2px（p＞0），点（10，12）代入抛物线方程求得p，进而求得
p
2
，即灯泡与反光镜的顶点的距离．
解答： 解：设抛物线方程为y2=2px（p＞0），点（10，12）在抛物线y2=2px上，
∴144=2p×10．
∴
p
2
=3.6．
因此，灯泡与反光镜的顶点的距离为3.6cm．
故选：C．
点评：本题主要考查了抛物线的应用和抛物线的标准方程．考查了对抛物线基础知识的掌握．
练习册系列答案
相关题目
化简：
tan(π-α)sin2(α+
π
2
)cos(2π-α)
cos3(-α-π)tan(α-2π)
．
已知数列{an}的首项为a1=5，前n项和为Sn，且Sn+1=2Sn+n+5（n∈N+）．
（1）证明：数列{an+1}是等比数列，并求数列{an}的通项公式；
（2）设关于x的函数f（x）=（a1+1）x+（a2+1）x2+…+（an+1）xn，求函数f（x）在点x=1处的导致f′（1）的值．
为了考察某公司生产的袋装牛奶的质量是否达标，从800袋牛奶中抽取60袋进行检验．利用随机数表抽取样本时，先将800袋牛奶按000，001，…，799进行编号，如果从随机数表的第8行第7列的数7开始向右读，则选出的第3袋牛奶的编号是
 
．（下面摘取了随机数表第7行至第9行的部分数据）
第7行  84　42　17　53　31　　57　24　55　06　88　　77　04　74　47　…
第8行  63　01　63　78　59　　16　95　55　67　19　　98　10　50　71　…
第9行  33　21　12　34　29　　78　64　56　07　82　　52　42　07　44　…
求不等式|x-2|-|x-1|＞0的解集．
已知函数f（x）=lnx+cosx-（
6
π
-
9
2
）x的导数为f′（x），且数列{an}满足an+1+an=nf′（
π
6
）+3（n∈N*）．
（1）若数列{an}是等差数列，求a1的值：
（2）若对任意n∈N*，都有an+2n2≥0成立，求a1的取值范围．
定义：若m-
1
2
＜x≤m+
1
2
（其中m是整数），则m叫做距实数x最近的整数，记作（x），即（x）=m，对于函数f（x）=|x-（x）|的五个命题，其中正确的有
 
（写出所有正确命题的序号）．
①函数y=f（x）的值域是[0，+∞）；
②函数y=f（x）是偶函数；
③函数y=f（x）是周期函数且最小正周期是1；
④函数y=f（x）的递增区间是[k，k+
1
2
]，k∈z；
⑤函数y=f（x）-lgx有4个零点．
若不等式x2-ax+1≥0对于一切a∈[-2，2]恒成立，则x的取值范围是
 
．
已知O是△ABC的外心，AB=6，AC=10，若
AO
=x
AB
+y
AC
，且2x+10y=5，则△ABC的面积为（　　）
A、24
B、
20
2
3
C、18或
20
2
3
D、24或20
2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网