题目内容
7.已知集合$A=\left\{{x\left|{{2^x}>\frac{1}{2}}\right.}\right\}$,B={x|x-1>0},则A∩(∁RB)={x|-1<x≤1}.分析 求出A与B中不等式的解集分别确定出A与B,找出A与B补集的交集即可.
解答 解:由A中不等式变形得:2x>$\frac{1}{2}$=2-1,
解得:x>-1,即A={x|x>-1},
由B中不等式解得:x>1,即B={x|x>1},
∴∁RB={x|x≤1},
则A∩(∁RB)={x|-1<x≤1},
故答案为:{x|-1<x≤1}
点评 此题考查了交、并、补集的混合运算,熟练掌握各自的定义是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.函数f(x)=lg(2x-1)的定义域为( )
| A. | (0,+∞) | B. | [0,+∞) | C. | [1,+∞) | D. | (0,1) |
16.定义$[\begin{array}{l}{{a}_{1}}&{{a}_{2}}\\{{b}_{1}}&{{b}_{2}}\end{array}]$=a1b2-a2b1,f(x)=$[\begin{array}{l}{\sqrt{3}sinxcosx+co{s}^{2}x}&{\sqrt{3}}\\{cos(\frac{3}{2}π+2x)}&{1}\end{array}]$,则f(x)( )
| A. | 有最大值1 | B. | 图象关于直线x=-$\frac{π}{6}$对称 | ||
| C. | 在区间(-$\frac{π}{6}$,0)上单调递增 | D. | 周期为π的偶函数 |
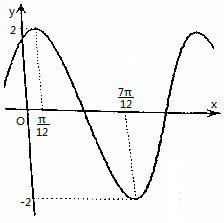 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|≤π),在一个周期内的图象如图.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|≤π),在一个周期内的图象如图.